Aplicação | Oficial de Justiça Avaliador

Trata-se de método específico para estimar a depreciação de máquinas e equipamentos (Caires, p. 171).

As equações desse método levam em consideração o fator de desgaste, a idade e a vida útil do equipamento.

O desgaste, por sua vez, varia em função da intensidade do trabalho a que a máquina foi submetida durante seu tempo de uso; esse desgaste, porém, pode ser atenuado caso o bem tenha recebido manutenção adequada. A função desgaste observa a seguinte equação:

$\begin{tabular}{llll} \\ & \multicolumn{3}{l}{\phi ( \mu, \tau ) = a \cdot e^{b \tau + c \mu + d \tau \mu}} \\ \end{tabular}$

$\begin{tabular}{llll} \\ & \mu & = & coeficiente de manutenção \\ & \tau & = & coeficiente de trabalho \\ & & & \\ \end{tabular}$

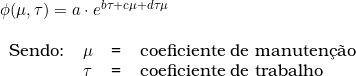
As constantes a, b, c, e d foram calculadas pelo desenvolvedor do método:

$\begin{tabular}{llll} \\ & a & = & 0,853081710 \\ & b & = & 0,067348748 \\ & c & = & -0,041679277 \\ & d & = & -0,001022860 \\ \end{tabular}$

A constante $\textsl{e}$ corresponde à base dos logaritmos naturais, calculada a partir da seguinte equação: $e = \left (1 + \dfrac{1}{n} \right )^n$

O fator de desgaste varia em função da intensidade de trabalho a que a máquina é submetida; todavia, esse desgaste pode ser desacelerado de acordo com as práticas de manutenção adotadas.

O fator calculado pela função desgaste é inserido na equação principal do método:

$D(t,\mu,{\tau},T) = \dfrac{A}{1 + B \codt e^{{\phi(\mu,\tau)} \cdot {C} \cdot t \slash T}} \\$

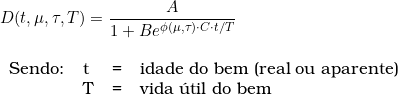
As constantes A, B e C foram calculadas pelo desenvolvedor do método:

$\begin{tabular}{llll} \\ & A & = & 1,347961431 \\ & B & = & 0,347961431 \\ & C & = & 3,579760093 \\ \end{tabular}$

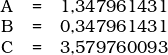
E, por fim:

$\begin{tabular}{llll} & \multicolumn{3}{l}{V_d = V_0 \cdot f_d } \\ \vspace{0.5cm} \\ Sendo: & V_d & = & valor do bem depreciado \\ & V_0 & = & valor do bem em estado de novo \\ & f_d & = & fator de depreciação \\ \end{tabular}$

Esse método também é compatível com ajustes de depreciação inicial e valor residual.

A planilha principal desenvolvida a partir desse método encontra-se disponível ao final deste texto.

Além dessa planilha, também se encontram disponíveis as seguintes tabelas, cada uma em sua página própria:

fatores de desgaste

E, também, os respectivos fatores de depreciação para as hipóteses de:

A planilha principal do método Caires pode ser acessada abaixo.

Método de depreciação Caires

Fonte:
CAIRES, Hélio Roberto Ribeiro. Novos tratamentos matemáticos em temas de engenharia de avaliações. São Paulo: Pini, 1977.