Os fatores de desgaste aplicados no método de depreciação Caires são calculados como o resultado de uma função de duas variáveis independentes:
-
- intensidade de trabalho ao qual o equipamento foi submetido
- qualidade das práticas de manutenção que foram adotadas
Os coeficientes dessas variáveis são introduzidos na equação da função desgaste. Deve ser observado que, quanto maior for a intensidade do trabalho ao qual o equipamento foi submetido, maior será o desgaste e, por consequência mais acentuada será a depreciação.
Por sua vez, quanto mais sofisticadas forem as práticas de manutenção para reduzir o desgaste, menor será a depreciação da máquina.
O método Caires considera:
-
- cinco níveis de intensidade de trabalho, cada qual correspondendo a um coeficiente específico; e
- cinco níveis de práticas de manutenção, cada qual, também, correspondendo a um coeficiente próprio.
Esses coeficientes, quando são cruzados entre si, geram vinte e cinco resultados à disposição do avaliador.
Ao cruzarmos esses coeficientes, analisando-se a variação do fator de desgaste em função da intensidade de trabalho ao qual o equipamento foi submetido, temos o seguinte gráfico:
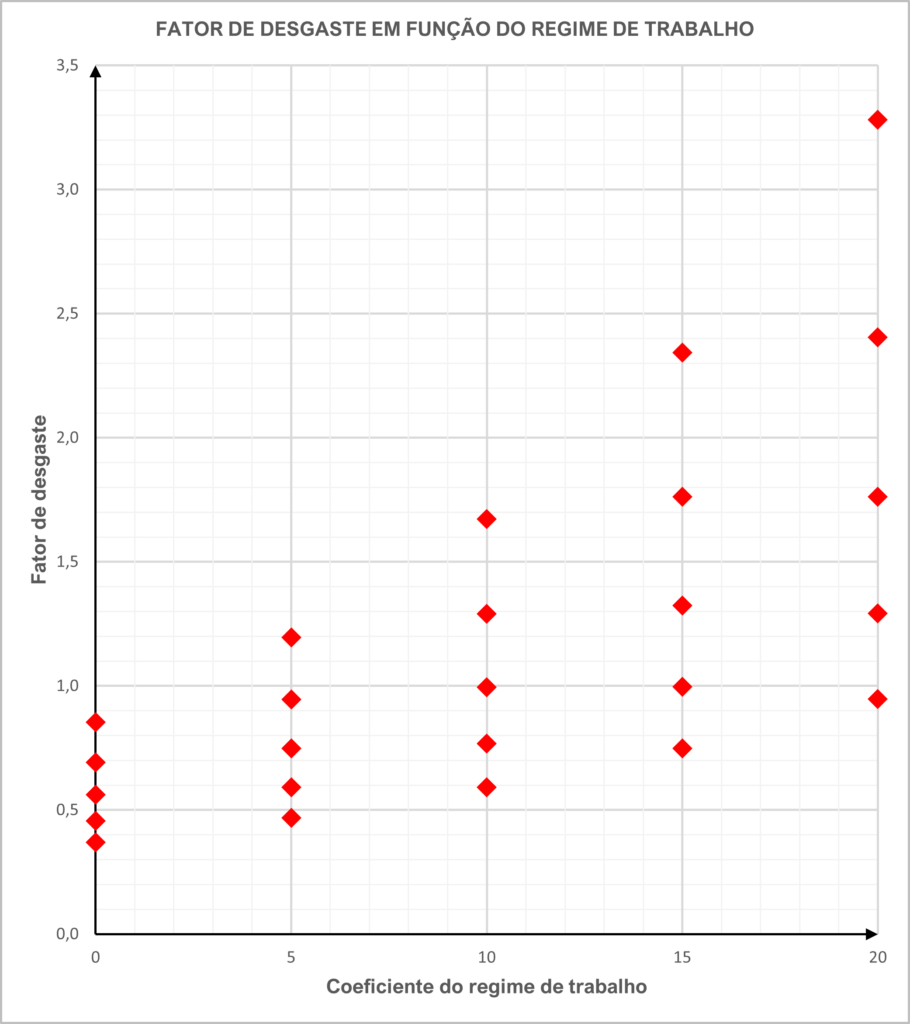
Observe-se que, ao aumentar a intensidade do trabalho, isso resulta em um desgaste maior.
Por sua vez, ao cruzarmos os mesmos coeficientes, analisando-se a variação do fator de desgaste em função da prática de manutenção que foi adotada, temos o seguinte gráfico:
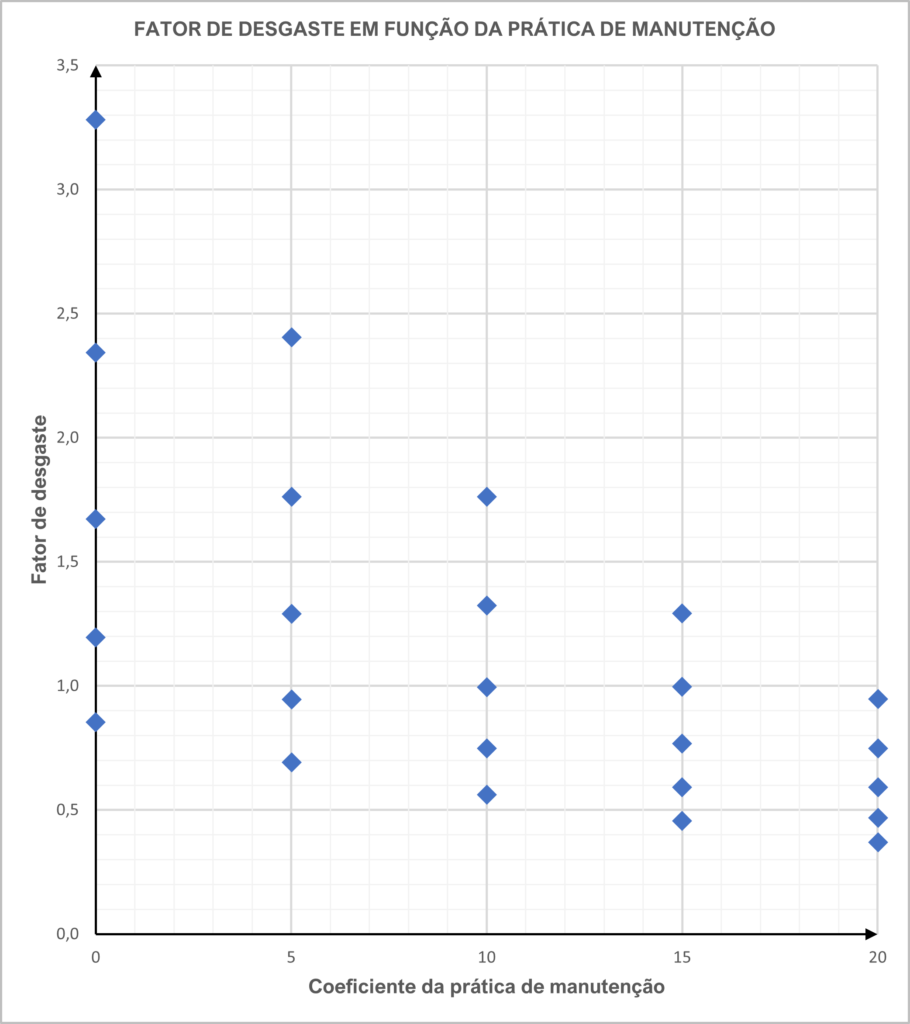
Observe-se que, ao aumentar o coeficiente atribuído à prática de manutenção, o desgaste é menor.
Associando-se os dois gráficos acima em um único de três dimensões, temos a seguinte superfície:
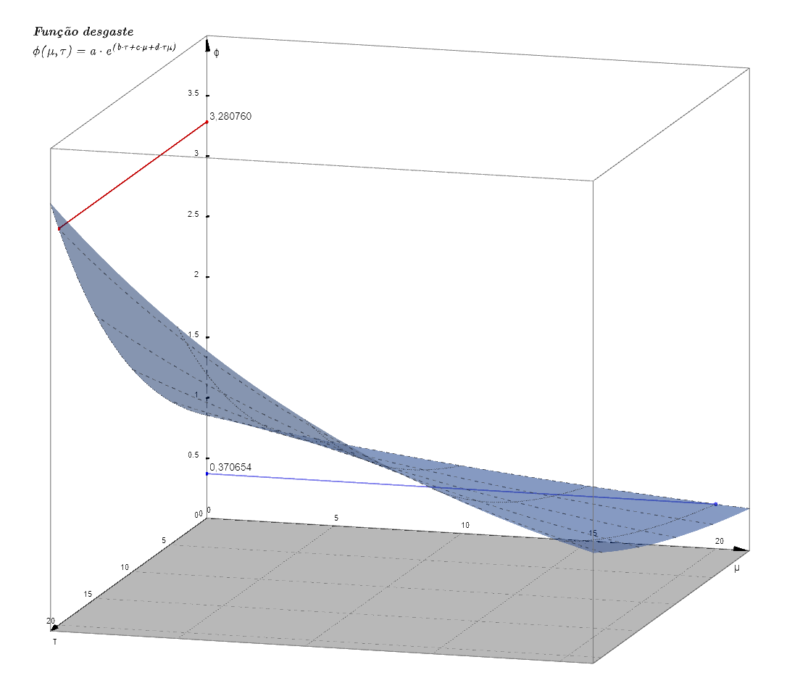
Abaixo, o perfil desse gráfico, a partir da variação das notas atribuídas às práticas de manutenção:
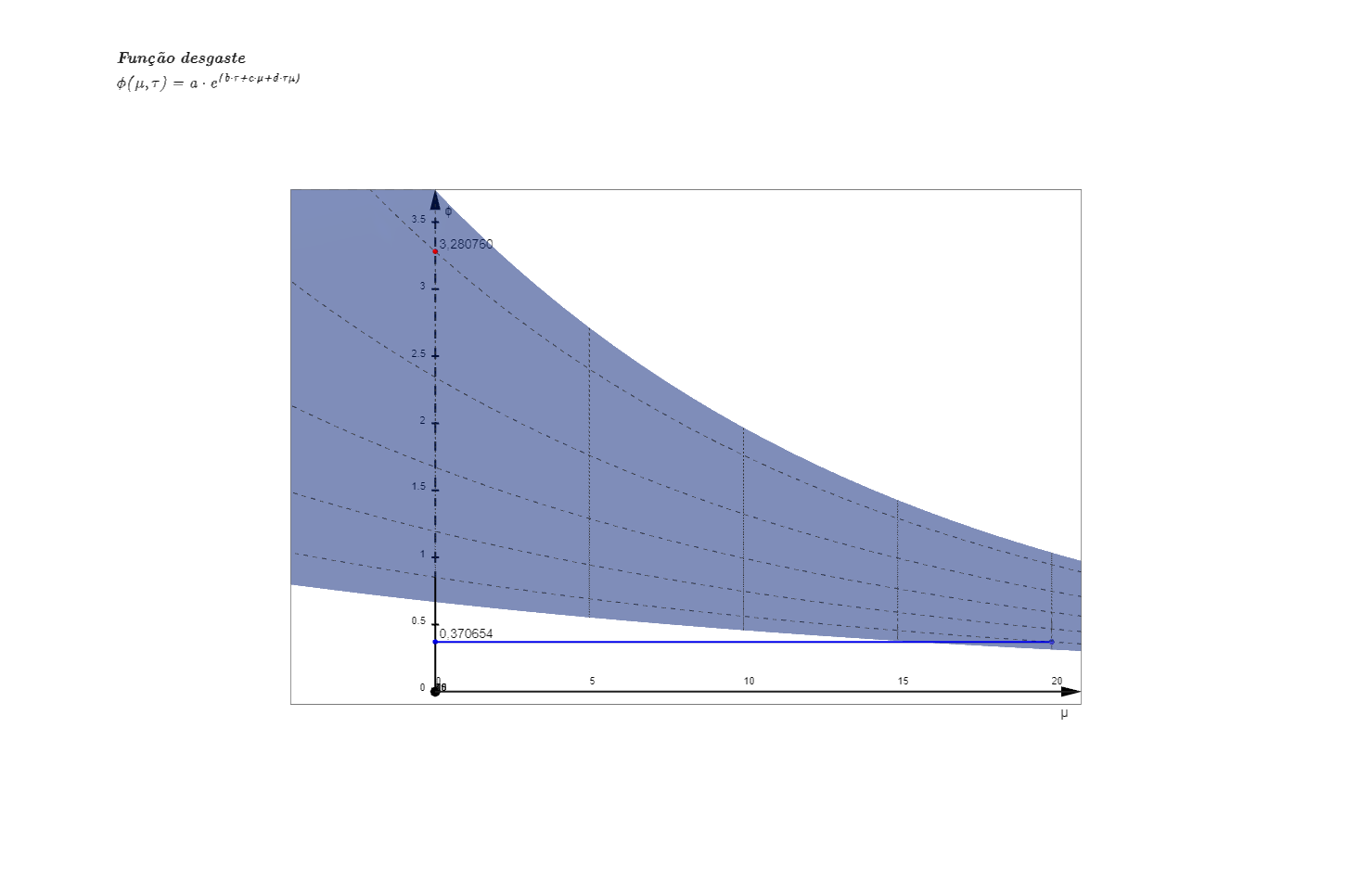
E, a seguir, o perfil do mesmo gráfico a partir da variação das notas atribuídas à intensidade de trabalho a que a máquina foi submetida:
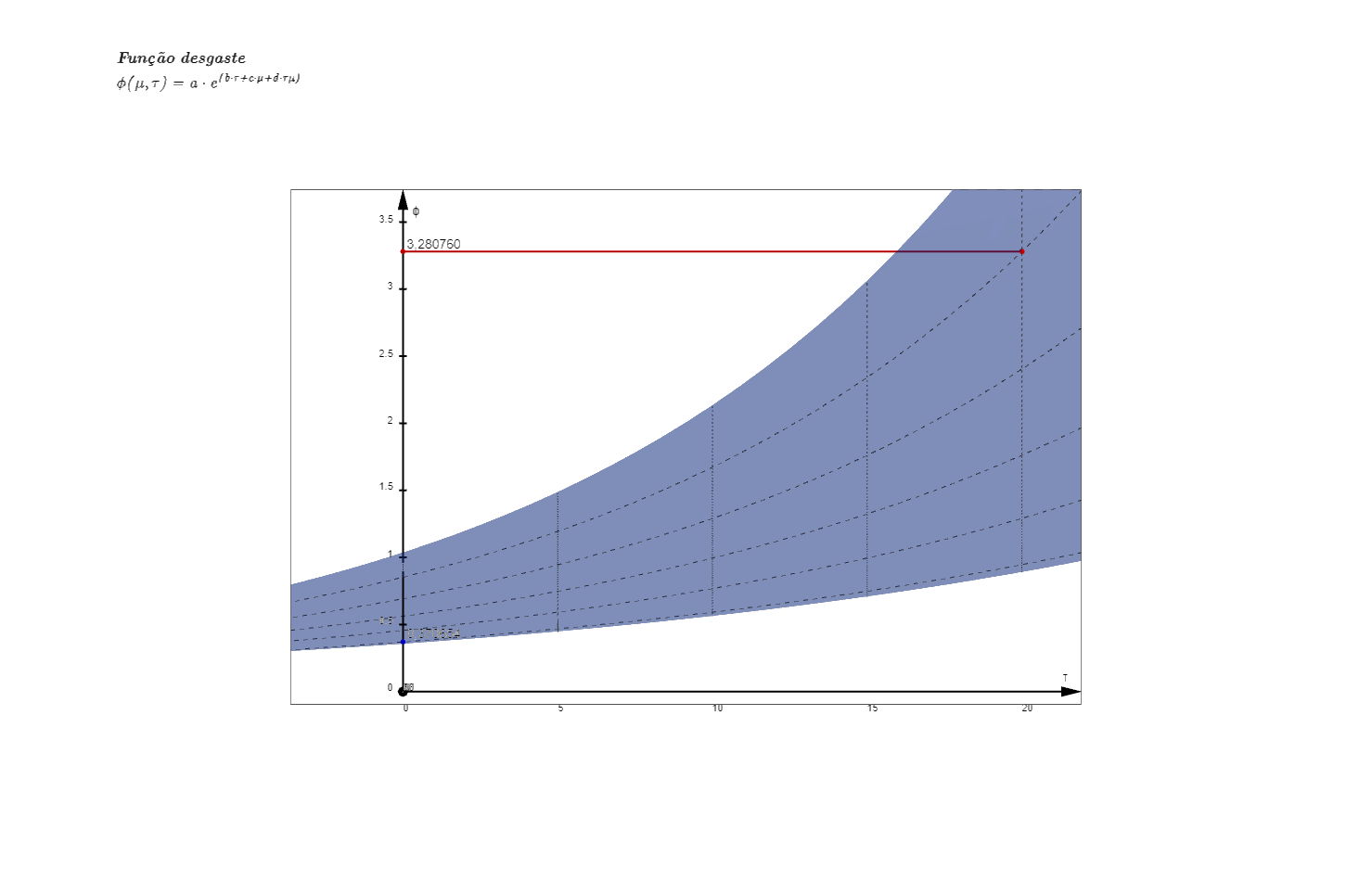
Nos gráficos acima é possível visualizar os pontos extremos da função desgaste:
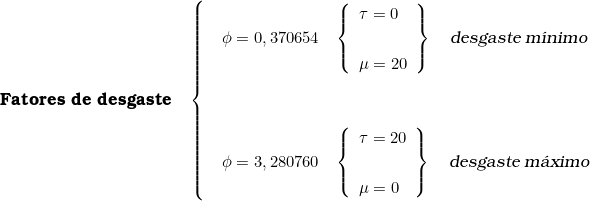
Abaixo, a tabela dos fatores de desgaste do método Caires.
A planilha principal do método Caires pode ser acessada abaixo.
Fonte:
CAIRES, Hélio Roberto Ribeiro. Novos tratamentos matemáticos em temas de engenharia de avaliações. São Paulo: Pini, 1977.

