Soma dos dígitos decrescentes

Por esse modelo, a depreciação é variável, diminuindo seu valor na medida em que os anos passam. Os adeptos desse método argumentam que sua utilização se faz necessária porquanto nos primeiros anos de utilização do bem as despesas de manutenção são menores por se tratar de um bem novo. Por sua vez, a eficiência do equipamento é total. Portanto, os recursos gerados podem suportar uma taxa de depreciação menor. Com o passar dos anos, a eficiência do equipamento se reduz, também em virtude da obsolescência natural e o seu custo de manutenção é maior, o que faz com que a máquina produza menos, o que justificaria uma quota de depreciação menor (SANTOS, Cleônimo. Depreciação do ativo imobilizado: aspectos práticos. 5. ed. São Paulo Folhamatic: IOB, 2013, p. 54).

Esse método, também conhecido como método Cole ou método da série, baseia-se em uma depreciação serial na forma:

 

\dfrac{n}{1+2+3+\ldots+n} \quad , \quad \dfrac{n-1}{1+2+3+\ldots+n} \quad , \quad \dfrac{n-2}{1+2+3+\ldots+n} \quad , \quad \ldots \quad, \quad \dfrac{1}{1+2+3+\ldots+n} \\ \vspace{0.5cm} \\ \text{A depreciação acumulada ao longo da idade do bem é calculada pela seguinte fórmula: } \\ \vspace{0.5cm} \\ D_a = \dfrac{t \cdot (2n - t + 1) \cdot D_p}{2} \\ \begin{tabular}{lll} Onde: & t & = idade do bem \\ & n & = vida útil do bem \\ & D_p & = \textup{depreciação por período} \end{tabular} \\ \vspace{1cm} \\ \text{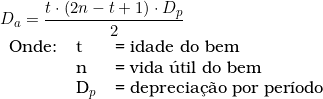A depreciação por período é calculada pela seguinte fórmula:} \\ \vspace{0.5cm} \\ D_p = \dfrac{2 \cdot (V_{novo} - V_r)}{n(n + 1)} \\ \begin{tabular}{lll} \\ Onde: & V_{novo} & = valor do bem novo \\ & V_r & = \textup{valor residual} \end{tabular}

 

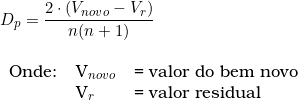
A planilha desenvolvida a partir desse método encontra-se disponível abaixo.

Método dos dígitos decrescentes

 

 

 

Fonte:
SANTOS, Cleônimo. Depreciação do ativo imobilizado: aspectos práticos. 5. ed. São Paulo Folhamatic: IOB, 2013.