Nesse método, a depreciação também é variável. No entanto, ele é inverso ao método […] (dígitos decrescentes). A cada ano, a depreciação vai aumentando, até consumir totalmente o bem objeto da depreciação. Os defensores do método da soma dos dígitos crescentes argumentam que sua utilização se faz necessária porquanto nos primeiros anos de utilização do bem o desgaste é menor, o que justificaria uma depreciação menor nos primeiros anos de sua utilização. (SANTOS, Cleônimo. Depreciação do ativo imobilizado: aspectos práticos. 5. ed. São Paulo Folhamatic: IOB, 2013, p. 55-56).
Esse método se baseia em uma depreciação serial na forma:
![]()
A depreciação acumulada ao longo da idade do bem é calculada pela seguinte fórmula:

A depreciação por período é calculada pela seguinte fórmula:
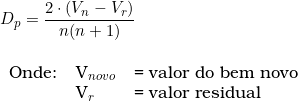
A planilha desenvolvida a partir desse método encontra-se disponível abaixo.
Fonte:
SANTOS, Cleônimo. Depreciação do ativo imobilizado: aspectos práticos. 5. ed. São Paulo Folhamatic: IOB, 2013.

