Conforme exposto por Gujarati, uma das premissas importantes do modelo de regressão linear clássico é que a variância de cada termo de erro ui, condicionado aos valores selecionados das variáveis explanatórias, é algum número constante igual a σ2. Essa é a premissa da homocedasticidade, ou seja igual (homo) espalhamento (cedasticidade), isto é, igual variância.
A homocedasticidade é um dos pressupostos do modelo de regressão linear e a exigência de que essa análise seja feita consta na NBR 14653-2:2011, A.2.1.3:
A verificação da homocedasticidade pode ser feita, entre outros, por meio dos seguintes processos:
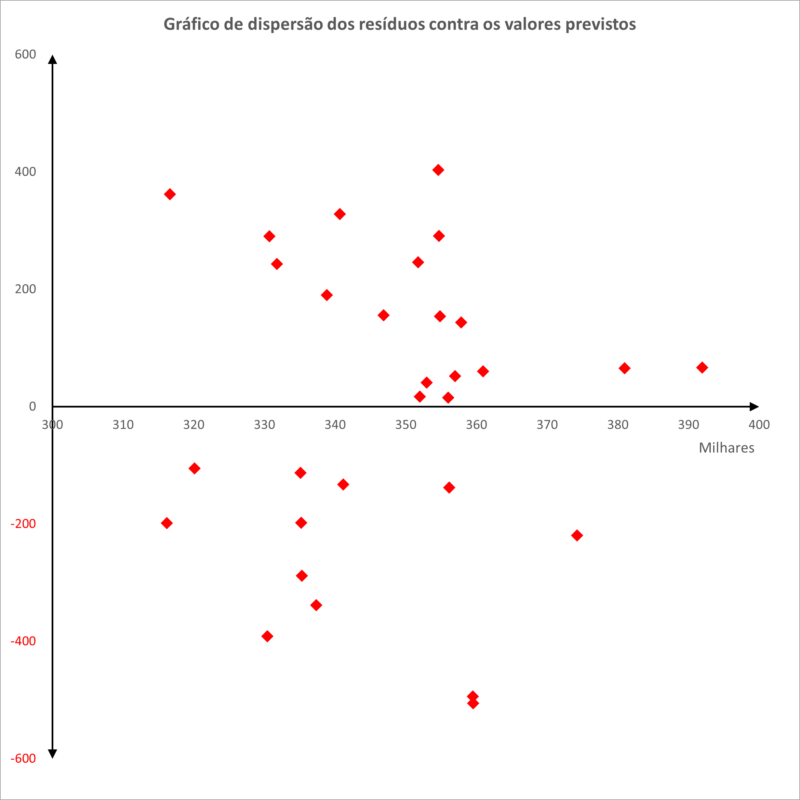
a) análise gráfica dos resíduos versus valores ajustados, que devem apresentar pontos dispostos aleatoriamente, sem nenhum padrão definido;
b) pelos testes de Park e de White
A NBR 14653-3:2019, em seu item A.2.2.3, traz exigência semelhante.
Entretanto, Gujarati faz uma advertência quanto ao teste de White no sentido de que, se o modelo tiver vários regressores, então a inclusão de todos os regressores, seus termos ao quadrado (ou a potências mais elevadas) e seus produtos cruzados podem consumir rapidamente os graus de liberdade e, por conta disso, é necessário ter cautela ao aplicar esse teste.
Com relação ao teste de Park, Gujarati (2006, p. 326), citando Goldfeld e Quandt, adverte que o termo de erro vi que entra na equação de regressão daquele teste pode não atender às pressuposições dos MQO e ser ele próprio heterocedástico.
O teste de Koenker-Bassett se apresenta como sendo uma alternativa válida, uma vez que está embasado nos quadrados dos resíduos; porém, em lugar de usá-los em uma regressão contra um ou mais regressores, é feita uma regressão dos quadrados dos resíduos contra os valores estimados do regressando elevados ao quadrado (NASSER JÚNIOR, 2019, p. 60). Portanto:

A preferência pelo teste de Koenker-Bassett se deve, ainda, ao fato de que esse teste pode ser aplicado com qualquer número de regressores.
No exemplo apresentado na planilha a análise de heterocedasticidade foi feita a partir do teste de Koenker-Bassett, onde os quadrados dos resíduos foram regredidos contra os quadrados dos valores previstos.
Neste momento, é necessário observar que a NBR 14653-2:2011, em seu item A.3, A.3.1. e a NBR 14653-3:2019, em seu item A.3, A.3.1 dispõem que o nível de significância máximo admitido nos demais testes estatísticos não deve ser superior a 10% (dez por cento).
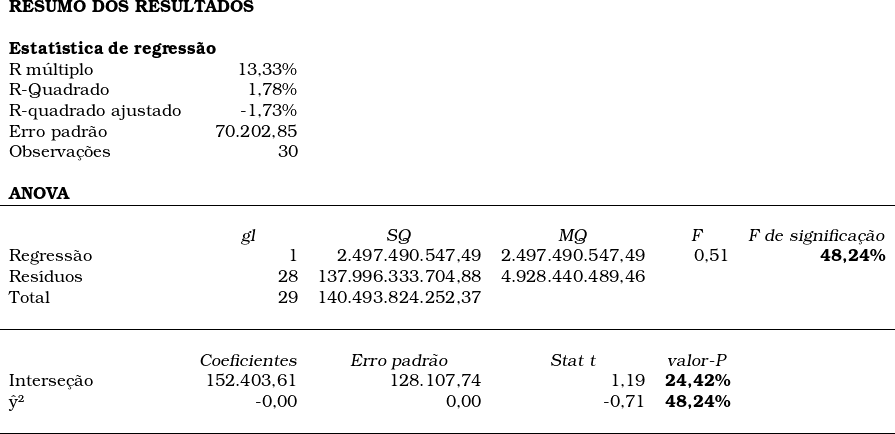
No exemplo contido na planilha, o nível de significância F foi superior a 10% (dez por cento), portanto a hipótese nula não pode ser rejeitada; por consequência, não se aceita o modelo.
Quanto ao nível de significância do coeficiente regressor, ele foi superior a 10% (dez por cento), portanto não se pode rejeitar a hipótese nula, ou seja, não se pode afirmar com segurança estatística que os resíduos dependem da variação dos valores previstos.
A par disso, também foi feita uma análise a partir do gráfico de dispersão e não foi detectado nenhum padrão definido entre os resíduos e os valores previstos pela regressão.
A planilha onde o teste foi desenvolvido está disponível abaixo.
Regressao-linear.-Analise-de-heterocedasticidade.-Teste-de-Koenker-Bassett.
Fontes:
GUJARATI, Damodar. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
______. Econometria: princípios, teoria e aplicações práticas; tradução de Cristina Yamagami; revisão técnica de Salvatore Benito Virgilito. São Paulo: Saraiva Educação, 2019.
NASSER JÚNIOR, Radegaz. Avaliação de bens: princípios básicos e aplicações. 3. ed. São Paulo: Editora Leud, 2019.

