A autocorrelação significa que, colocando os dados em uma série ordenada, os respectivos resíduos estariam correlacionados com os anteriores ou com os posteriores nessa série. Por isso, esse problema também é conhecido como correlação serial.
A exigência para que se faça essa verificação está em NBR 14653-2:2011:
A.2.1.4 Verificação da autocorrelação
O exame de autocorrelação deve ser precedido pelo pré-ordenamento dos elementos amostrais, em relação aos valores ajustados e, se for o caso, às variáveis independentes possivelmente causadoras do problema.
Sua verificação pode ser feita, entre outros procedimentos, pela análise do gráfico de resíduos cotejados com os valores ajustados, que deve apresentar pontos dispersos aleatoriamente, sem nenhum padrão definido.
A NBR 14653-3:2019, em seu item A.2.2.4 traz essa exigência semelhante.
Para detectar esse problema, o Eng. Nasser Júnior faz referência a Gujarati. Em Econometria básica, Gujarati afirma que o teste mais famoso para a detecção de correlação serial é o desenvolvido pelos estatísticos Durbin e Watson e é conhecido como estatística d de Durbin-Watson (2006, p. 376).
A fórmula do método é:
![]()
a qual, após ser desenvolvida, resulta em:
![]()
Posteriormente, o resultado da fórmula acima é analisado de acordo com os critérios de decisão:

O gráfico onde os resíduos foram comparados contra os elementos amostrais filtrados em ordem crescente será apresentado abaixo. Apesar de o gráfico não apresentar nenhum padrão definido entre os resíduos e os elementos amostrais, o problema também foi analisado pelo teste de Durbin-Watson.
A planilha com o exemplo está disponível abaixo, logo após o gráfico.
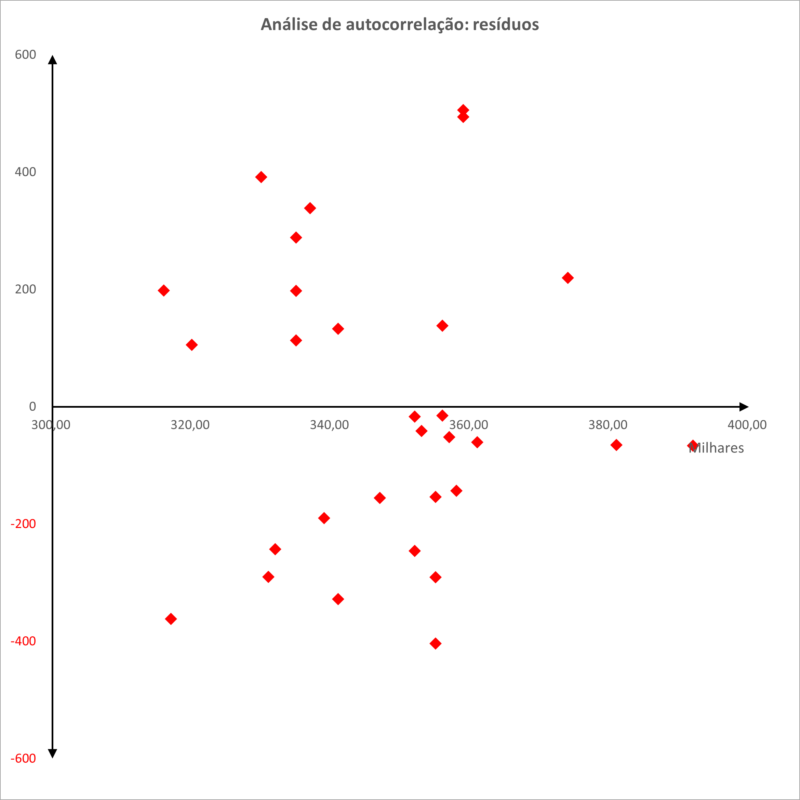
A planilha com o exemplo utilizado nesta página está disponível logo abaixo:
Análise de autocorrelação. Teste de Durbin-Watson
Fontes:
GUJARATI, Damodar. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006, p. 376 e 786-789.
NASSER JÚNIOR, Radegaz. Avaliação de bens: princípios básicos e aplicações. 3. ed. São Paulo: Editora Leud, 2019, p. 65-66.
OLIVEIRA, Ana Maria de Biazzi Dias; GRANDISKI, Paulo. Métodos científicos e a engenharia de avaliações (com ênfase em inferência estatística). In: Engenharia de avaliações v. 1, 2. ed. São Paulo: Liv. e Ed. Universitária de Direito, 2014, p. 83.

