Fator profundidade

A NBR 14653-2:2019 apresenta os conceitos de frente projetada, frente real e de profundidade equivalente:

3.27: frente projetada: projeção da frente real sobre a normal ao menor dos lados ou a corda, no caso de frente em curva
3.28 frente real: comprimento efetivo da linha divisória do imóvel com a vida de acesso, em projeção horizontal
[…]
3.58 profundidade equivalente: resultado numérico da divisão da área de um lote pela sua frente projetada principal

Portanto:

p_e = \dfrac{S}{f_{proj}}

O cálculo do fator de profundidade depende da relação entre a profundidade equivalente do terreno, a profundidade mínima e a profundidade máxima da zona; existem cinco hipóteses de cálculo e, para cada uma delas, uma fórmula própria.

A planilha que foi desenvolvida abrange as cinco hipóteses. A princípio, devemos conhecer o valor de cada uma das variáveis abaixo:

\begin{tabular}{lll} \\ p_e & = & profundidade equivalente \\ p_{mínima} & = & profundidade mínima para a zona \\ p_{máxima} & = & profundidade máxima para a zona \\ p & = & expoente (tabelado) \\ \end{tabular}

 

Nos exemplos abaixo, consideraremos o valor do expoente p como sendo 0,50, haja vista a Tabela 1, Grupo 1 da Norma para avaliação de imóveis urbanos IBAPE-SP 2011.

1ª Hipótese

p_e \leqslant \dfrac{p_{mínima}}{2} \\ \vspace{0.5cm} \\ Fórmula: \qquad f_p = \left( \dfrac{1}{2} \right)^p

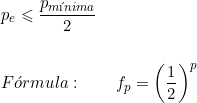
2ª Hipótese

\dfrac{p_{mínima}}{2} \leqslant p_e \leqslant p_{mínima} \\ \vspace{0.5cm} \\ Fórmula: \qquad f_p = \left( \dfrac{p_{mínima}}{p_e} \right)

 

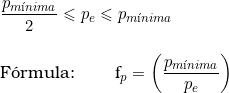
3ª Hipótese

{p_{mínima}} \leqslant p_e \leqslant p_{máxima} \\ \vspace{0.5cm} \\ Fórmula: \qquad f_p = 1

 

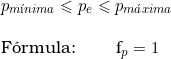
4ª Hipótese

p_{máxima} \leqslant p_e \leqslant 3 \cdot p_{máxima} \\ \vspace{0.5cm} \\ Fórmula: \qquad f_p = \dfrac{1} {\dfrac{p_{máxima}}{p_e} + \left[1- \left(\dfrac{p_{máxima}}{p_e} \right) \right] \cdot \left( \dfrac{p_{máxima}}{p_e} \right)^p}

 

5ª Hipótese

p_e \ge 3 \cdot p_{máxima} \\ \vspace{0.5cm} \\ Fórmula igual à fórmula da hipótese 4, considerando \qquad p_e = 3 \cdot p_{máxima} \\ \vspace{0.5cm} \\ f_p = \dfrac{1}{\dfrac{p_{máxima}}{p_e} + \left[ 1- \left( \dfrac{p_{máxima}}{p_e} \right) \right] \cdot \left( \dfrac{p_{máxima}}{p_e} \right)^p},\ ou\ seja: \\ \vspace{0.5cm} \\ \dfrac{1}{\dfrac{p_{máxima}}{3 \cdot p_{máxima}} + \left [1 - \left( \dfrac{p_{máxima}}{3 \cdot p_{máxima}} \right) \right] \cdot \left( \dfrac{p_{máxima}}{3 \cdot p_{máxima}} \right) ^p},\ ou\ seja\ \\ \vspace{0.5cm} \\ \dfrac{1}{\dfrac{1}{3}+\left[1 - \left( \dfrac{1}{3} \right) \right] \cdot \left( \dfrac{1}{3} \right)^p}

 

A variação do fator de profundidade pode ser visualmente demonstrada no seguinte gráfico:

 

 

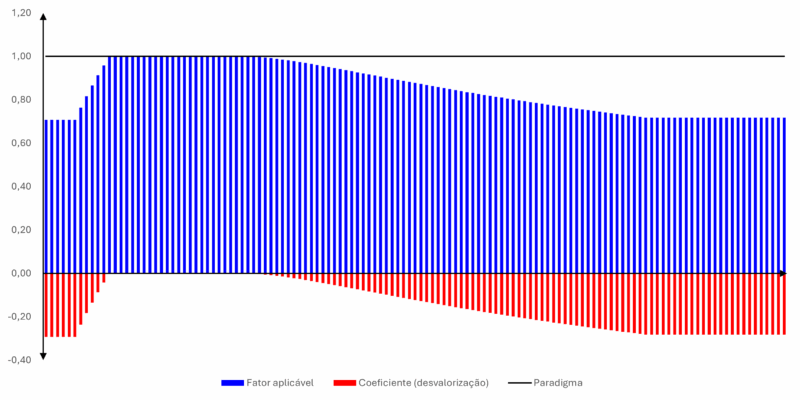
A planilha desenvolvida para calcular o fator de profundidade identifica qual é a hipótese aplicável e, de imediato, informa o coeficiente (de valorização ou de desvalorização) e o respectivo fator que deverá ser aplicado na tabela de homogeneização.

A planilha está disponível logo abaixo.

Planilha para cálculo do fator de profundidade e da profundidade equivalente

 

 

 

Fontes:
ABUNAHMAN, Sérgio Antônio. Curso básico de engenharia legal e de avaliações. 4. ed. revista e ampliada. São Paulo: Pini, 2008.
FIKER, José. Manual de avaliações e perícias em imóveis urbanos. 4. ed. São Paulo: Pini, 2016.
THOFEHRN, Ragnar. Avaliação de terrenos urbanos: por fórmulas matemáticas. São Paulo: Pini, 2008.