O saneamento é um procedimento utilizado para se analisar a dispersão dos dados da amostra e, por consequência, homogeneizá-la se for necessário; nesse etapa do processo de avaliação, a partir de critérios objetivos previamente estabelecidos, identificam-se os pontos atípicos, ou seja, eventuais elementos estranhos à massa de dados (NBR 14653-2:2011, item 3.48); como efeito do saneamento, teremos uma amostra mais homogênea, com um coeficiente de variação menor.
O saneamento pode ser feito a partir do critério de Chauvenet: calcula-se o intervalo de valores admissíveis e se exclui o elemento que ultrapassar os limites desse intervalo.
Por fim, analisa-se cada item amostra contra os limites do intervalo, excluindo-se aquele que os extrapolar.
O valor 
é calculado pelas seguintes equações:
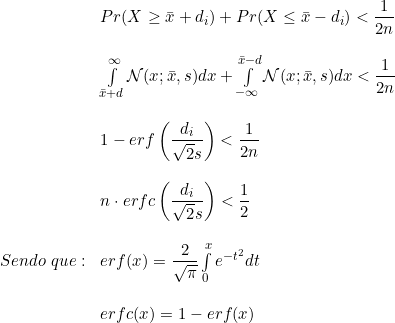
Caso mais de um elemento ultrapasse os limites do intervalo, exclui-se aquele que mais se distanciar da média do conjunto, um por vez; após se faz nova análise.
Os limites do intervalo são calculados pelo número de desvios-padrão admissíveis, o qual varia em função do tamanho da amostra. Na tabela de valores tabelados, 
representa o tamanho da amostra: Tabela dos valores críticos do critério de Chauvenet.
A cada etapa de saneamento, reduzem-se a dispersão dos dados e, por consequência, o coeficiente de variação. O exemplo abaixo é continuidade da homogeneização apresentada na página: Homogeneização por fatores.
Na primeira etapa do saneamento, temos a seguinte situação:
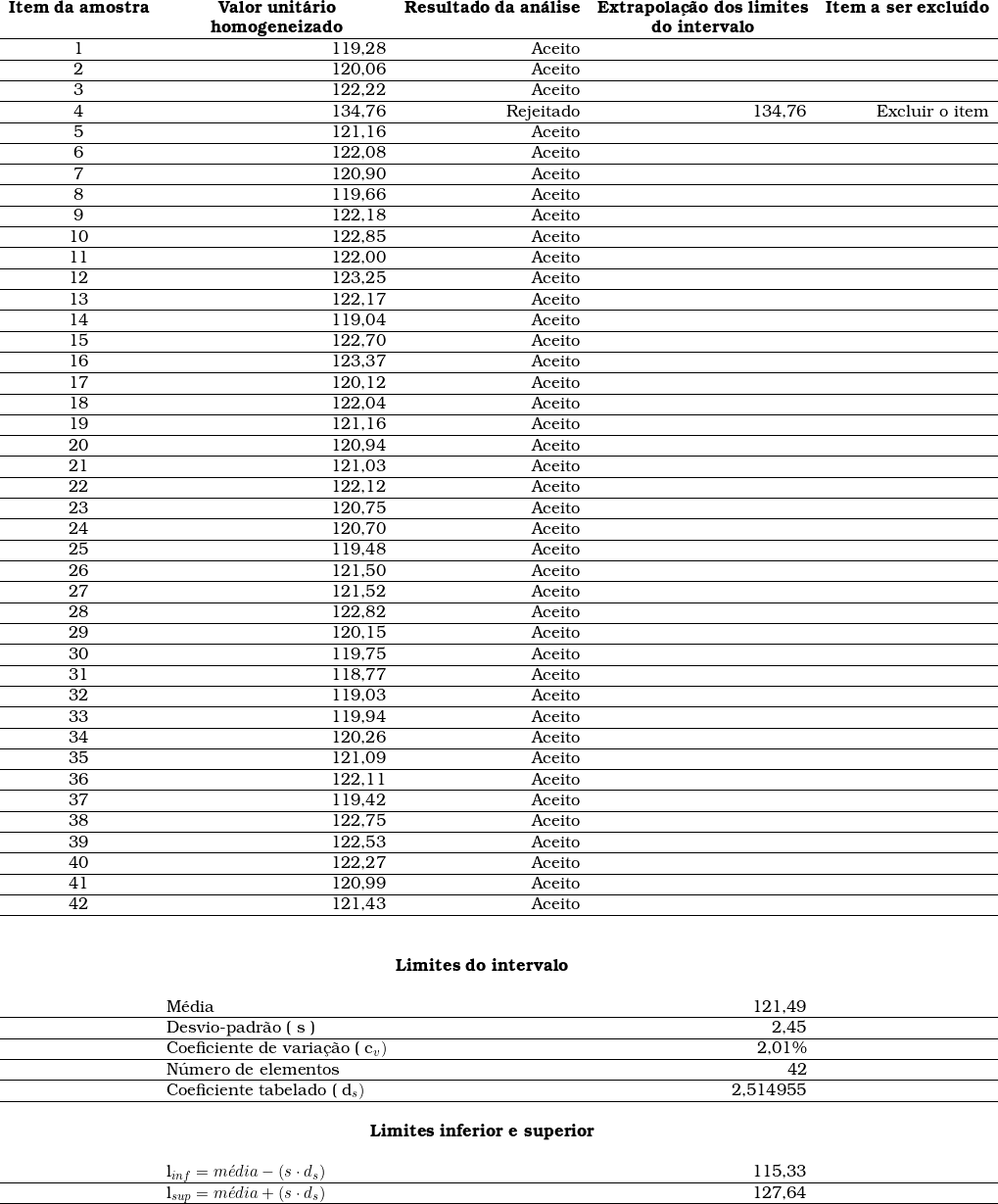
Nessa etapa, a dispersão de dados pode ser demonstrada com o seguinte gráfico:
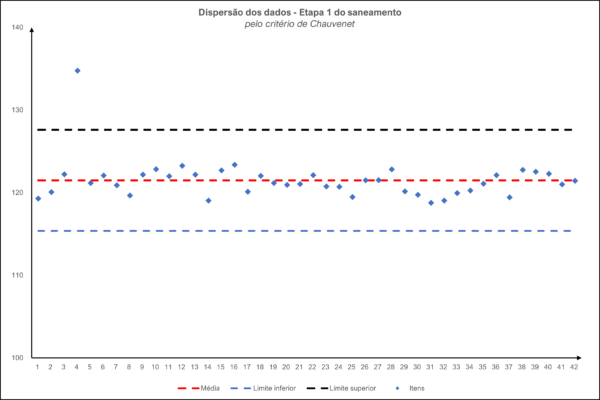
O quarto item extrapolou o limite superior, sendo portanto um ponto atípico que deverá ser excluído do conjunto de dados.
Passamos, então, para segunda etapa do saneamento, onde temos a seguinte situação:
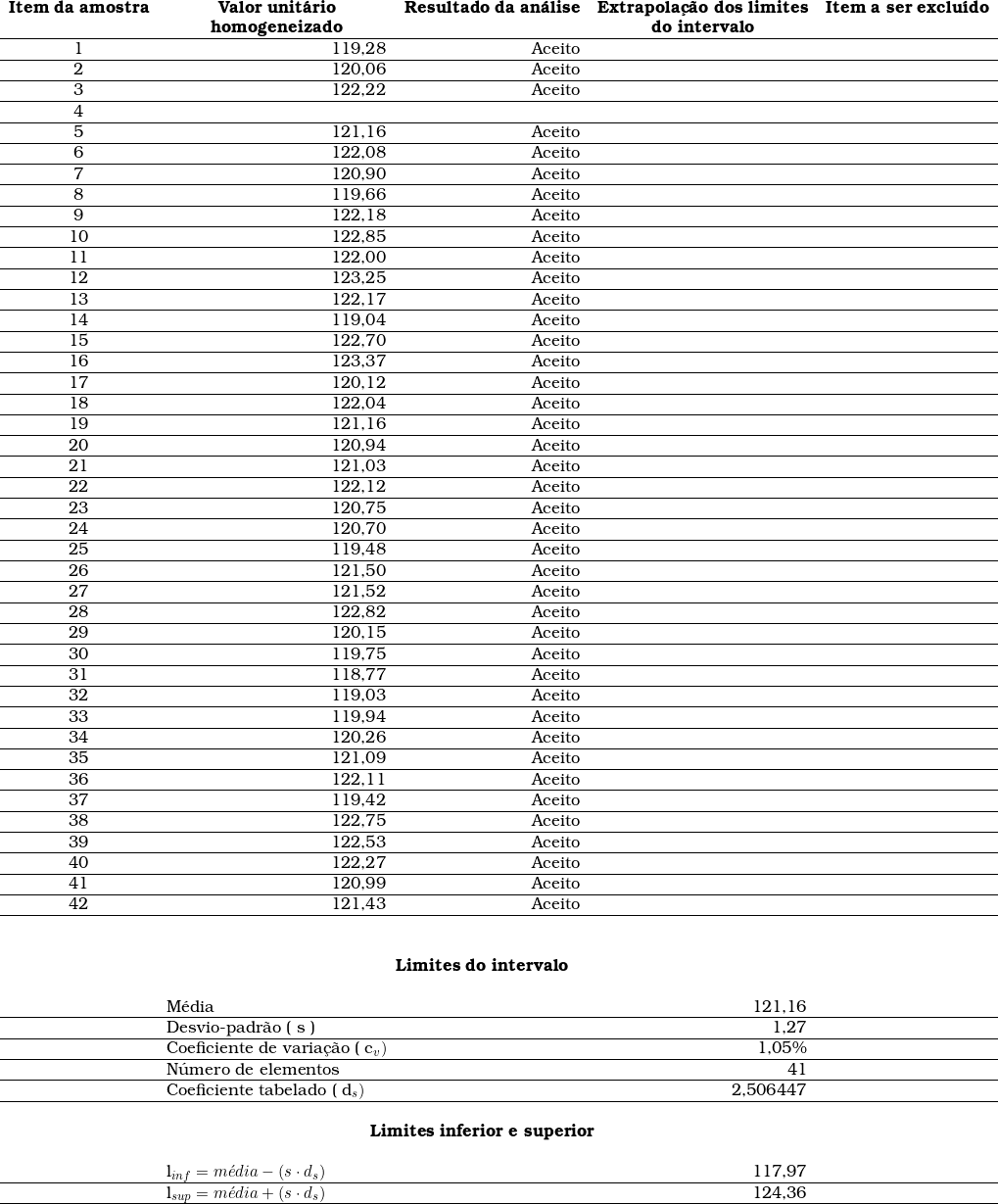
A dispersão dos dados diminuiu e isso pode ser comprovado objetivamente pela análise do coeficiente de variação ( cv ), que foi reduzido.
Todos os elementos encontram-se dentro dos limites do intervalo, conforme pode ser visualizado no gráfico abaixo:
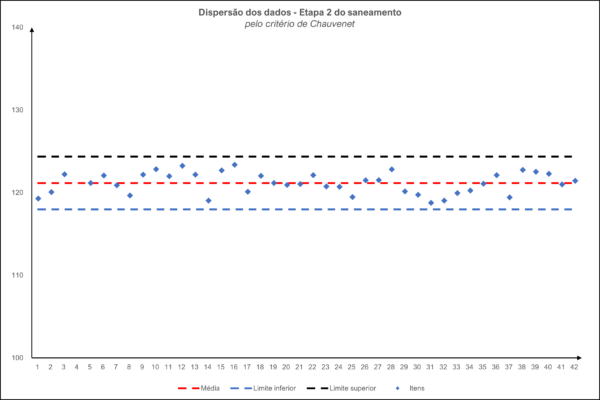
Todos os elementos estão contidos dentro dos limites do intervalo; portanto, encerra-se o saneamento.
A planilha desenvolvida para esse procedimento encontra-se disponível abaixo.
Saneamento da amostra pelo critério de Chauvenet
Fontes:
LIMA, Marcelo Rossi de Camargo. Engenharia de avaliações aplicada em propriedades rurais: tratamento científico e por fatores: perícias em desapropriações e servidões. São Paulo: Editora Leud, 2021.
NASSER JÚNIOR, Radegaz. Avaliação de bens: princípios básicos e aplicações. 3. ed. São Paulo: Editora Leud, 2019.
THOFEHRN, Ragnar. Avaliação de terrenos urbanos: por fórmulas matemáticas. São Paulo: Pini, 2008.
