Sinking fund depreciation method

Sobre esse método, temos na doutrina especializada:

Este método, que os norte-americanos chamam de sinking fund depreciation method, não é tão simples de se aplicar como o da linha reta, mas tem um fundamento mais racional.
De fato, o método da linha reta pressupõe o destaque anual de uma quantia fixa que, posta de lado e adicionada às demais e àquela resultante do valor residual, reproduza o custo inicial para aquisição de um novo bem no fim da vida útil daquele que está sendo depreciado.
Ora, é inconcebível que alguém simplesmente ponha anualmente no cofre essas quantias correspondentes à depreciação sem que elas rendam quaisquer juros.
Por isso, dizemos ser o método do fundo de amortização mais racional, uma vez que esse método prevê o depósito dessas quantias num fundo que renda juros compostos durante toda a vida útil do equipamento ou do bem.
No fim do período da vida útil, a quantia existente no fundo (principal mais juros) deverá ser igual à diferença entre o custo inicial e o valor residual. (MOREIRA, 2001, p. 233).

 

A equação abaixo fornece o valor da parcela anual de depreciação, seguindo os critérios específicos do método.

 

 

Abaixo, apresenta-se um exemplo de avaliação em que, ao final de cada período, o valor do bem foi atualizado a partir do .

 

 

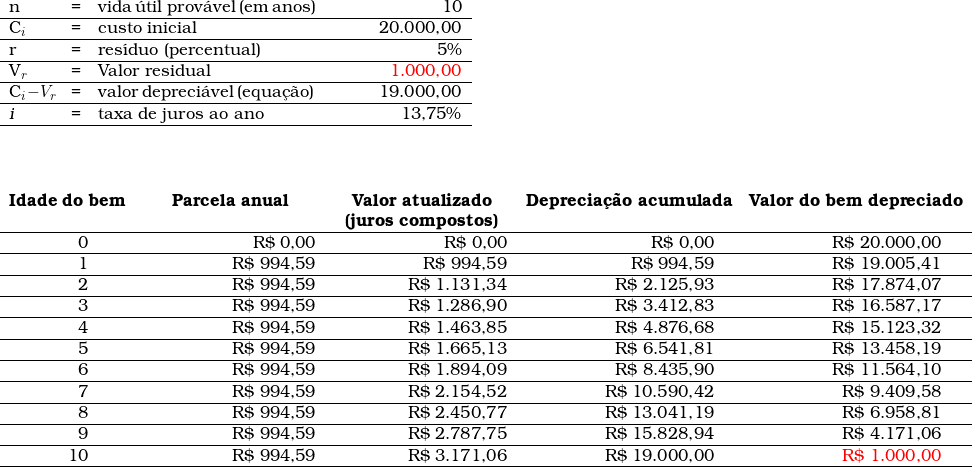
A planilha desenvolvida para a utilização desse método está disponível abaixo.

Sinking fund depreciation method

 

 

 

Fonte:
MOREIRA, Alberto Lélio. Princípios de engenharia de avaliações. 5. ed. revisada e ampliada. São Paulo: Pini, 2001.