Nesse procedimento, serão excluídos os itens cujo número de desvios-padrão ultrapassar os limites admissíveis. O tamanho da amostra determina qual é o nível de significância máximo admitido e, por sua vez, a amplitude da região de aceitação dos valores sob análise. Os valores máximo e mínimo do intervalo são calculados a partir do valores críticos de Arley.
A equação para se calcular o ri de cada item da amostra é:

Se ri > rcrítico, então o elemento i é um ponto atípico (outlier).
O valor de rcrítico é calculado com o auxílio da distribuição t de Student, com v igual a n – 2 graus de liberdade.
O gráfico abaixo demonstra a variação dos pontos r críticos em função dos graus de liberdade para cada um dos quatro níveis de significância, bem como a forma como eles se aproximam dos pontos tcríticos da distribuição de Student e dos pontos zcríticos da distribuição normal.
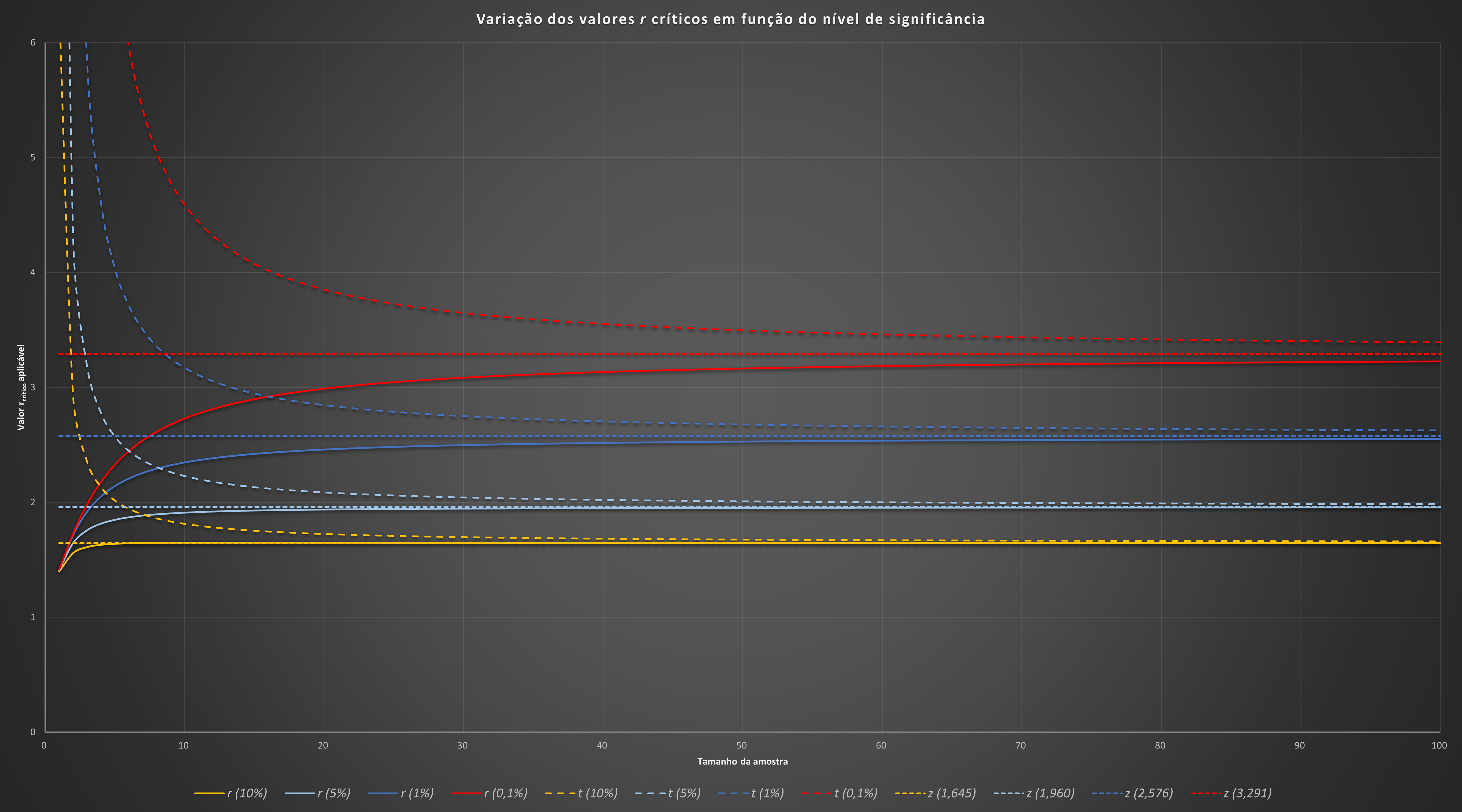
Fonte:
ARLEY, Niels; BUCH, Kai Rander. Introducción a la teoría de la probabilidad y de la estadística. Tradução: Fernando Bombal Gordón. Madrid: Editorial Alhambra S.A., 1968.

