Solução matricial

O objetivo desta seção é demonstrar as ferramentas matemáticas utilizadas para a solução de um sistema linear; essa demonstração é meramente didática, pois atualmente a solução de  um sistema linear se faz através de planilhas eletrônicas. 

Após a coleta e seleção dos dados que irão compor a amostra, constrói-se uma tabela semelhante a esta:

 

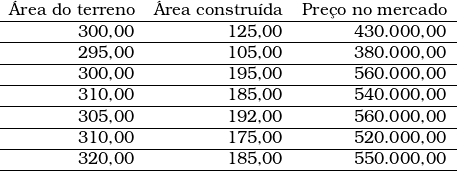
Podemos transformar essa amostra no seguinte sistema linear:

 

 

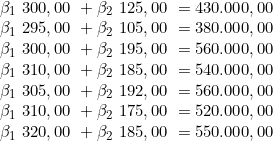
Nesse sistema, as matrizes principais são:

 

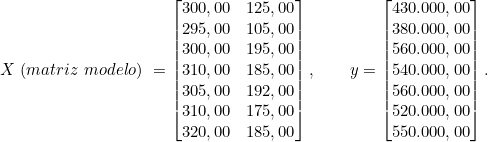
Cabe-nos, agora, calcular as incógnitas (coeficientes regressores) que resolvam o sistema linear acima, ou os valores que forneçam a melhor solução aproximada.

Na análise do sistema linear acima, será inserida uma coluna para representar a constante (intercepto); portanto, a matriz a ser utilizada nos cálculos será:

 

A solução matricial desse sistema é dada por:  onde:

 

Matriz transposta de :

 

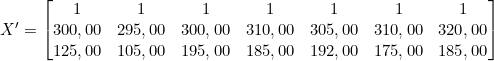
Resultado da multiplicação:

 

Inversão matricial:

 

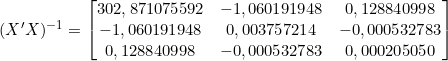
O elementos da diagonal principal da matriz são 302,871075592, 0,003757214 e 0,000205050.

Sendo:

 

Os coeficientes regressores são:

 

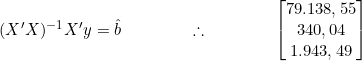
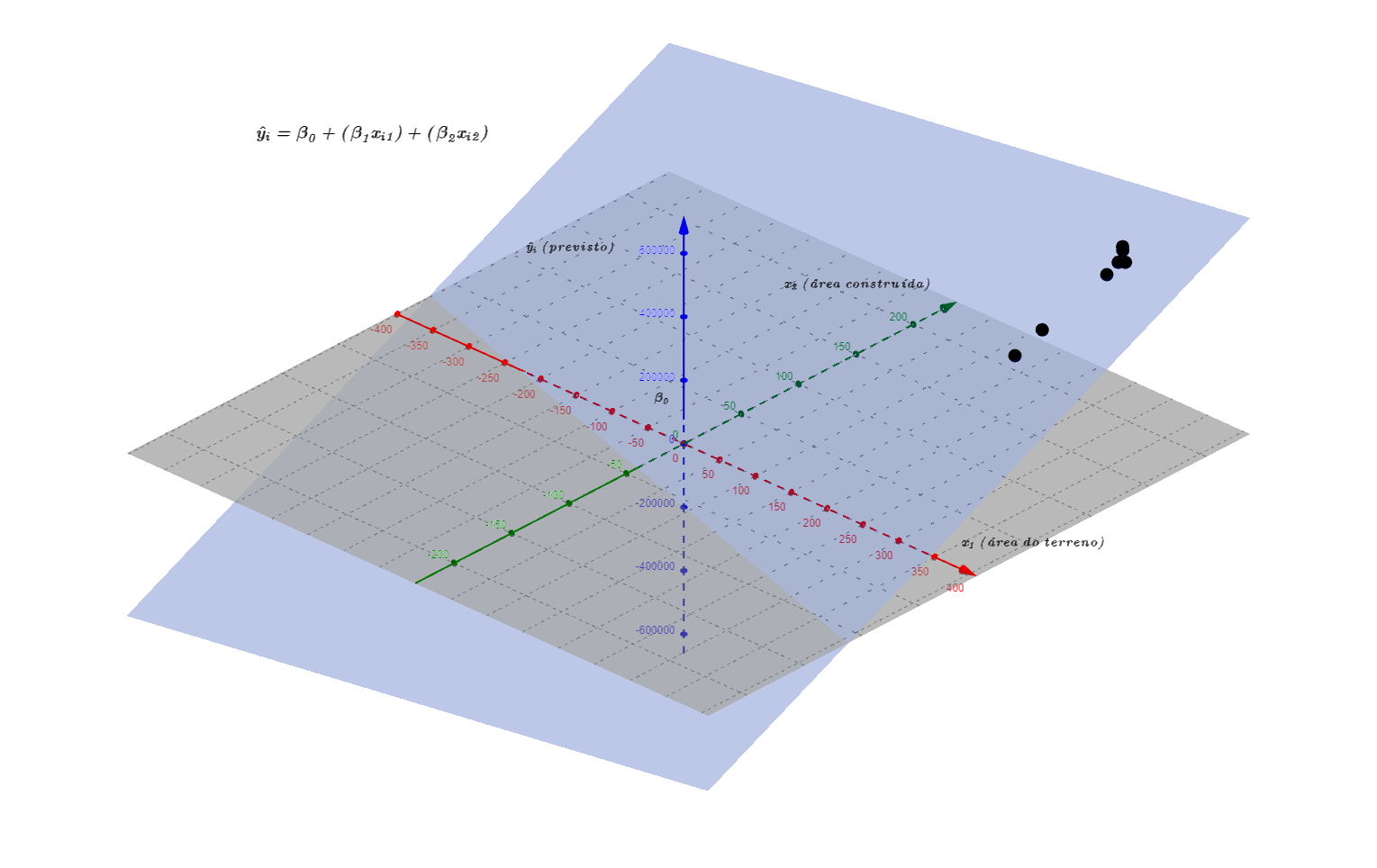
O gráfico que demonstra visualmente os resultados da regressão linear múltipla é o seguinte:

 

 

Cálculo do erro padrão da regressão

 

 

 

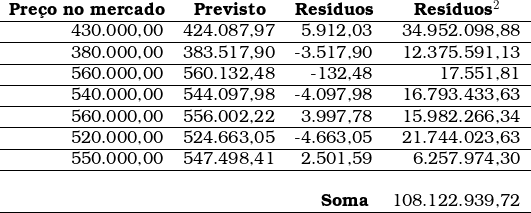
Cálculo do erro padrão de cada coeficiente regressor (incluindo o intercepto)

 

 

 

TESTES DE NÍVEL DE SIGNIFICÂNCIA (ERRO TIPO I)

Teste de nível de significância de cada regressor

A estatística-t é calculada pela razão entre o coeficiente regressor e o seu respectivo erro padrão:

 

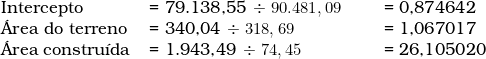
Nesse ponto, devemos observar as diretrizes contidas na NBR 14653-2:2011. Avaliação de bens. Parte 2: Imóveis urbanos. Item 9.2.1, tabela 1, item 5.

 

O nível de significância máximo estabelecido na norma é de 30% (trinta por cento), para o grau de fundamentação I.

A amostra do exemplo acima contém 7 elementos. No modelo matemático de análise dessa amostra foram consideradas 2 (duas) variáveis independentes, quais sejam: área do terreno e área construída, além do intercepto (constante).

Nessa configuração, o valor crítico é dado por:

 

Na configuração do exemplo, o valor crítico é 1,189567, conforme consta na tabela da distribuição-t de Student. Os resultados da regressão foram:

 

 

Portanto, em um nível de significância de 30% (trinta por cento), os coeficientes regressores do intercepto e da área do terreno se encontram na região de aceitação da hipótese nula, lembrando que nesse teste:

(1)  

 

No caso, a probabilidade de que é maior do que 30% (trinta por cento) e por isso, com relação a esses coeficientes, a hipótese nula não pode ser rejeitada.

Diga-se o mesmo em relação a .

A situação pode ser demonstrada visualmente nos dois primeiros gráficos abaixo; observe-se que o primeiro e o segundo coeficientes regressores se encontram na região de aceitação da hipótese nula (GUJARATI, 2006, p. 105).

 

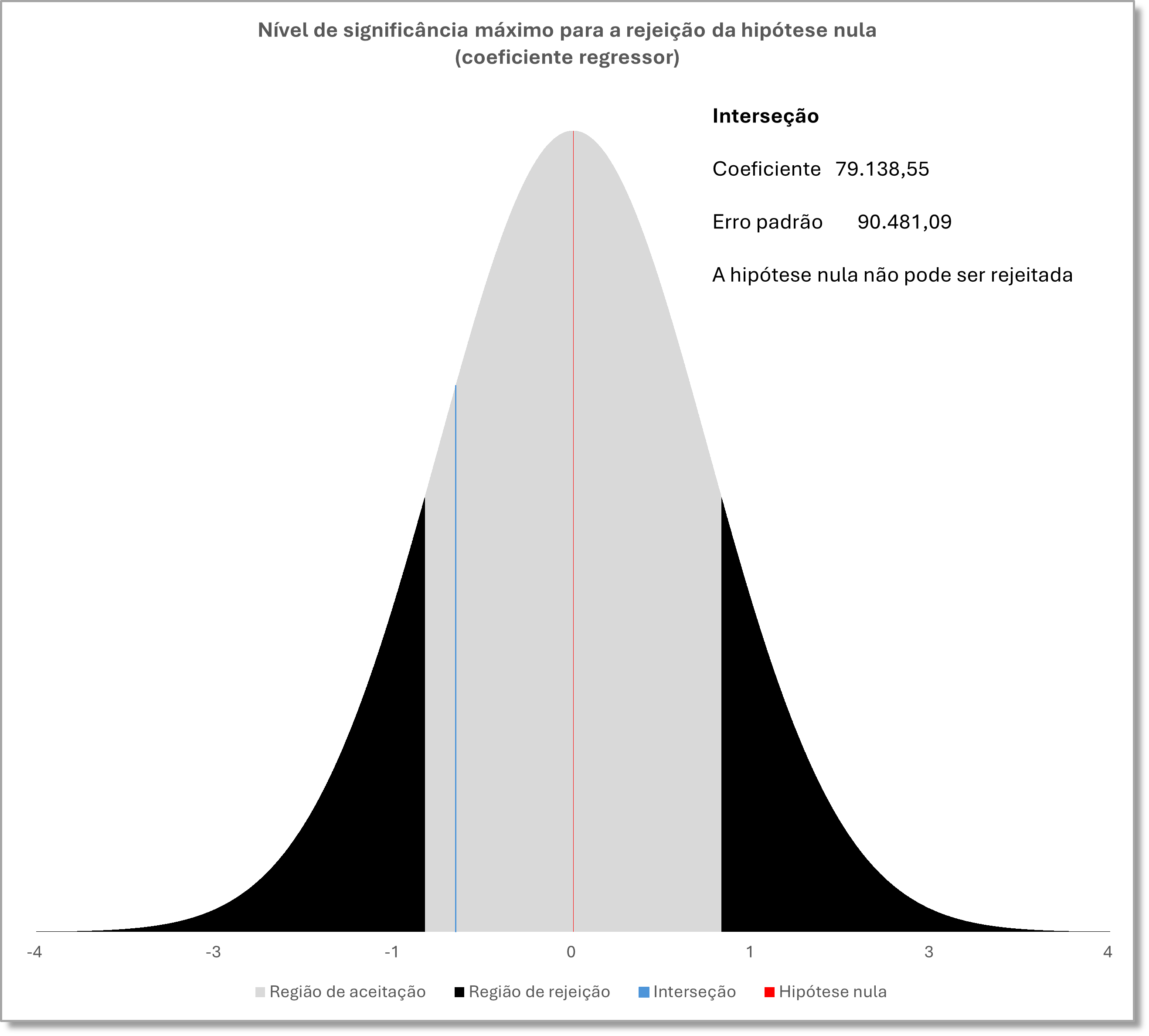
Interseção

O intercepto se encontra na área de aceitação da hipótese nula; portanto, em relação ao intercepto não se pode rejeitar a hipótese nula.

Desse modo, seguindo as orientações contidas nas normas NBR 14653-2:2011 e 14653-3:2019, o intercepto não é estatisticamente útil para o modelo adotado.

 

 

 

Coeficiente da variável independente: Área do terreno ( x₁ )

O coeficiente regressor relativo à variável independente área do terreno também se encontra na área de aceitação da hipótese nula; portanto, em relação ao seu respectivo coeficiente regressor, não se pode rejeitar a hipótese nula.

Desse modo, seguindo as orientações contidas nas normas NBR 14653-2:2011 e 14653-3:2019, a variável independente área do terreno não é estatisticamente útil para o modelo adotado.

 

 

 

 

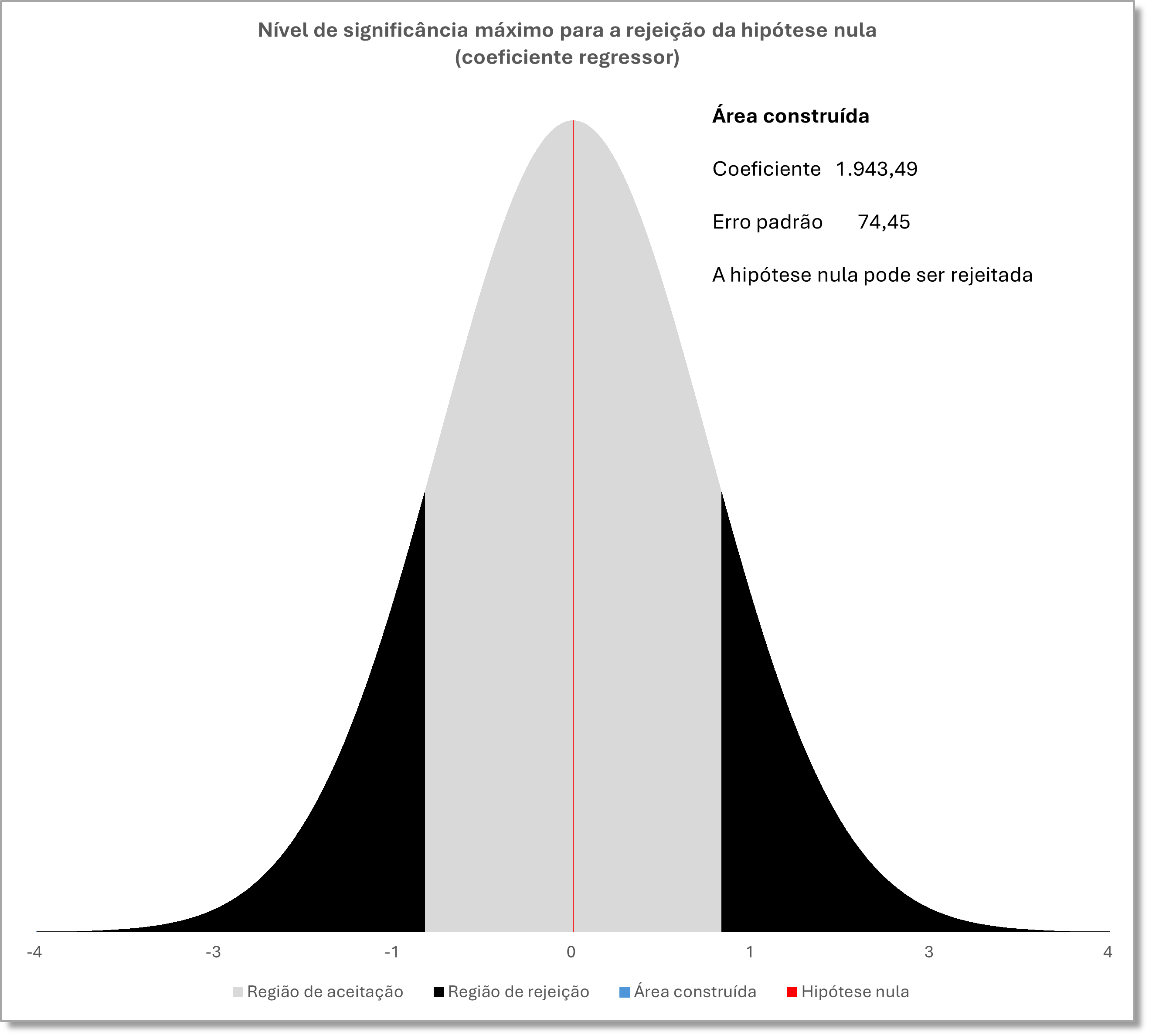
Coeficiente da variável independente: Área construída ( x₂ )

O coeficiente regressor relativo à variável independente área construída se encontra na área de rejeição da hipótese nula; portanto, em relação ao seu respectivo coeficiente regressor, pode-se rejeitar a hipótese nula.

Desse modo, seguindo a orientação contida nas normas NBR 14653–2:2011 e 14653-3:2019, afirma-se que  variável independente área construída é estatisticamente útil para o modelo adotado.

 

 

 

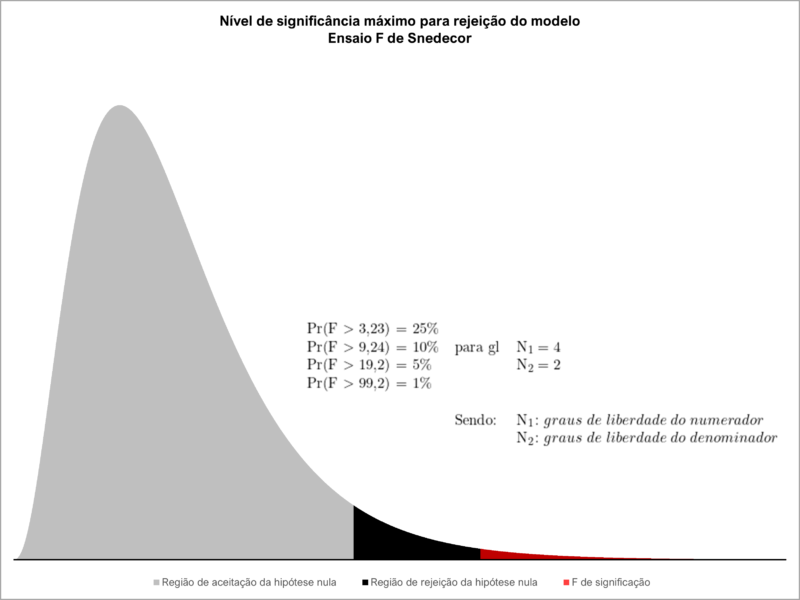
Teste de nível de significância do modelo (ensaio F de Snedecor)

Nesse ponto, devemos observar as diretrizes contidas na NBR 14653-2:2011. Avaliação de bens. Parte 2: Imóveis urbanos. Item 9.2.1, tabela 1, item 6.

 

 

O nível de significância máximo para a rejeição da hipótese nula, admitido na norma, é de 5% (cinco por cento), para o grau de fundamentação I.

 

 

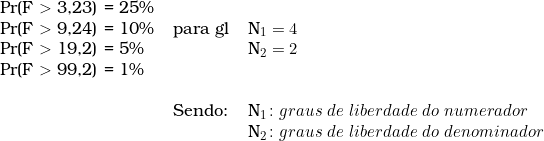
Os resultados indicam que a regressão atingiu o ponto 567,19 na estatística F, portanto superior a 19,2, que é o limite crítico fixado com base nos graus de liberdade do modelo, em um nível de significância máximo de 5% (cinco por cento). Pode-se, pois, rejeitar a hipótese nula do modelo.

Os pontos percentuais superiores estão disponíveis para consulta na página: Distribuição F.

O resultado do teste F de Snedecor (ou ensaio F de Snedecor) pode ser demonstrado visualmente no gráfico abaixo:

 

 

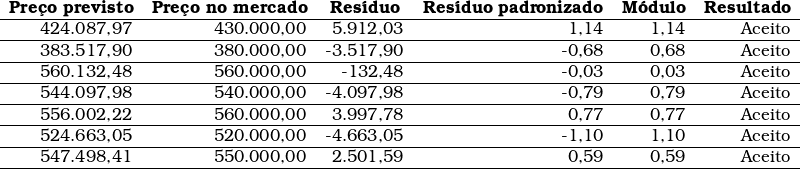
Análise de normalidade

 

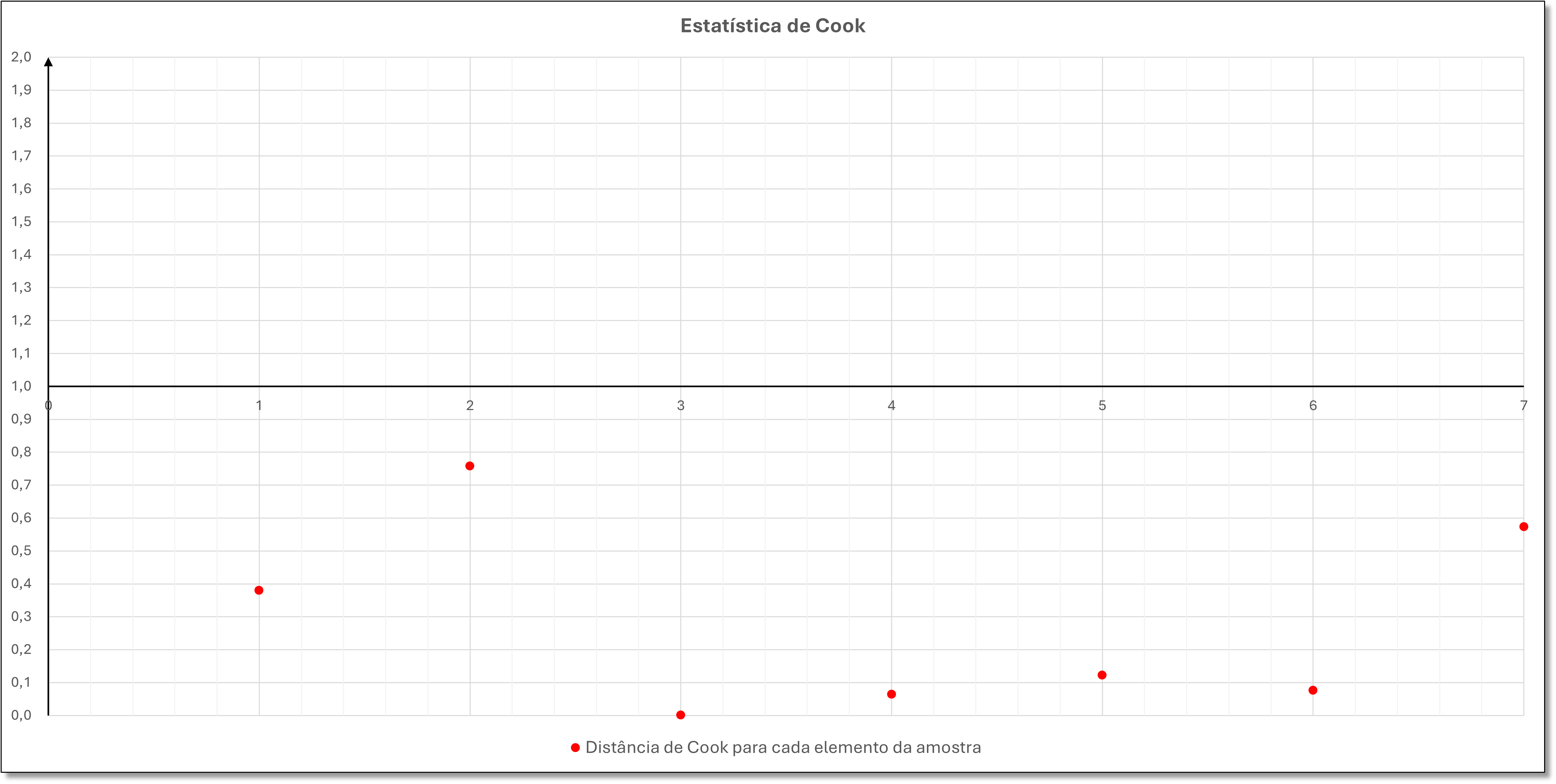
Distância de Cook

A análise detalhada dos resíduos será feita através do relatório gerado pelo programa SisDEA®.

Na doutrina, ao analisar os resultados da estatística de Cook, sugere-se o corte em 1 (um), baseado em uma regra prática (Anderson; Sweeney; Williams, 1999, p. 661).

Não foram detectados pontos influenciantes, pois todos os resultados da estatística de Cook ficaram abaixo de 1 (um), conforme pode ser visualizado no gráfico abaixo.

 

 

 

Os dados acima foram, também, analisados no programa Microsoft Excel® e no programa SisDEA®. Os relatórios gerados por esses programas estão disponíveis para consulta.