Conceito

Análise de regressão

A análise de regressão é de longe a técnica de dependência mais amplamente usada e versátil, aplicável em cada faceta da tomada de decisões em negócios. Seus usos variam desde os problemas mais gerais até os mais específicos, sendo que em cada caso relaciona um fator (ou fatores) a um resultado específico. Por exemplo, a análise de regressão é o fundamento para os modelos de previsão em negócios, variando de modelos econométricos que prevêem a economia nacional com base em certas informações (níveis de renda, investimentos e assim por diante) até modelos de desempenho de uma empresa em um mercado se uma estratégia específica de marketing for adotada. os modelos de regressão também são empregados para estudar como os consumidores tomam decisões ou formam impressões e atitudes. Outras aplicações incluem a avaliação de determinantes de efetividade de um programa (p. ex., quais fatores ajudam a manter a qualidade) e a determinação da viabilidade de um novo produto ou o retorno esperado de um novo empreendimento. Ainda que esses exemplos ilustrem apenas um pequeno subconjunto de todas as aplicações, eles demonstram que a análise de regressão é uma ferramenta analítica poderosa planejada para explorar todos os tipos de relações de dependência.
A análise de regressão múltipla é uma técnica estatística geral usada para analisar a relação entre uma única variável dependente e diversas variáveis independentes (HAIR JR et al., 2009, p. 149).

 

A análise de dados por modelo de regressão linear é considerada “uma das principais ferramentas da econometria”, sendo considerada a sua “pedra fundamental” (GUJARATI, 2019, p. 3).

 

NBR 14653-2:2011. Avaliação de bens. Parte 2. Imóveis urbanos. Anexo A (normativo) Procedimentos para a utilização de modelos de regressão linear

A.1 Introdução.
A.1.1 A técnica mais utilizada quando se deseja estudar o comportamento de uma variável dependente em relação a outras que são responsáveis pela variabilidade observada nos preços é a análise de regressão.
A.1.2 No modelo linear para representar o mercado, a variável dependente é expressa por uma combinação linear das variáveis independentes, em escala original ou transformadas, e respectivas estimativas dos parâmetros populacionais, acrescida de erro aleatório, oriundo de:
– efeitos de variáveis não detectadas e de variáveis irrelevantes não incluídas no modelo;
– imperfeições acidentais de observação ou de medida;
– variações do comportamento humano, como habilidades diversas de negociação, desejos, necessidades, compulsões, caprichos, ansiedades, diferenças de poder aquisitivo, diferenças culturais, entre outros.

 

Os mesmos termos se encontram no item A.1 da NBR 14653-3:2019. Avaliação de bens. Parte 3. Imóveis rurais e seus componentes.

Observando-se que “um sistema linear não envolve produtos ou raízes de variáveis. Todas as variáveis ocorrem somente na primeira potência e não aparecem, por exemplo, como argumentos de funções trigonométricas, logarítmicas ou exponenciais […] um conjunto finito de equações lineares é denominado um sistema de equações lineares ou, simplesmente, um sistema linear. As variáveis são denominadas incógnitas” (ANTON; RORRES, 2012, p. 2).

 

Modelo linear

O sistema linear descrito nas normas técnicas mencionadas acima pode ser expresso como:

 

 

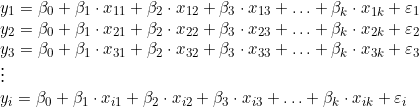
Na doutrina especializada, esse sistema é denominado modelo linear de Gauss-Markov (LUNA, OLINDA, 2014, p.95) ou modelo linear clássico (MARINHO, 2023, p. 80). 

A forma matricial do sistema acima é a seguinte:

 

ou simplesmente:

No sistema e nas matrizes acima, o índice do elemento foi anotado antes do índice da variável independente a ele relacionada (ANTON, RORRES, 2012, p. 6). 

As condições que devem ser preenchidas para a validação desse modelo (MARINHO, 2023,  p. 80) são:

1. média zero dos resíduos;
2. homocedasticidade dos resíduos (variância constante);
3. não-autocorrelação (independência serial dos resíduos);
4. normalidade dos resíduos;
5. não-aleatoriedade das variáveis independentes;
6. número de observações maior que o número de coeficientes a serem estimados; e
7. não existência de relação exata (colinearidade perfeita) entre quaisquer das variáveis independentes.

 

Sobre o pressuposto f devem ser observadas as diretrizes contidas na NBR 14653-2:2011 (Avaliação de imóveis. Parte 2: Imóveis urbanos), item 9.2.1, tabela 1, item 2, e na NBR 14653-3:2019 (Avaliação de bens. Parte 3: Imóveis rurais e seus componentes), item 9.3.1, tabela 2, item 2.

Modelo linear geral

Sobre o modelo linear, pode-se dizer que:

O modelo estatístico a adotar pode ser satisfeito por uma variedade de funções, sendo importante destacar, neste ponto que, se houver indicações de que o relacionamento estudado é linear – ou linearizável pela transformação nas escalas das variáveis envolvidas  -, ele poderia ser representado pela equação:  onde Y_i é uma variável dependente ou explicada (no caso específico, podendo ser definida pelo valor de um bem) explicada pela variação em conjunto de variáveis independentes ou explicativas X₁, X₂, …, X_k (que podem corresponder, por exemplo, aos principais atributos do bem, tais como, área, frente, topografia, localização, padrão, etc.) e por um termo aleatório εi, que representa:
• a natural oscilação de preços de mercado, inerentemente aleatória, em virtude da imprevisibilidade do comportamento humano, acrescida de
• todos os possíveis erros de mensuração ou informação de dados relevantes, e de
• todas as demais variáveis x_(k+1), x_(k+2), etc. que fetam os preços de mercado (a variável dependente), mas que não estão presentes no modelo, e que ficam incluídas no “erro”, também designado como “resíduo”. (OLIVEIRA; GRANDISKI, 2014, p. 66).

 

As transformações de variáveis mencionadas acima podem ser:

 

 

Ainda, sobre transformação de variáveis:

 

Deve-se, porém, observar as orientações contidas nos items A.9 da NBR 14653-2:2011 e A.9 da NBR 14653-3:2019, no sentido de que a variável dependente no modelo de regressão deve ser apresentada no laudo na forma não transformada.

O conjunto de dados abaixo será submetido à análise por regressão linear múltipla (duas variáveis independentes: área do terreno e área construída; com o acréscimo do intercepto), sem transformação das variáveis, ou seja, será utilizado o modelo linear geral: 

 

 

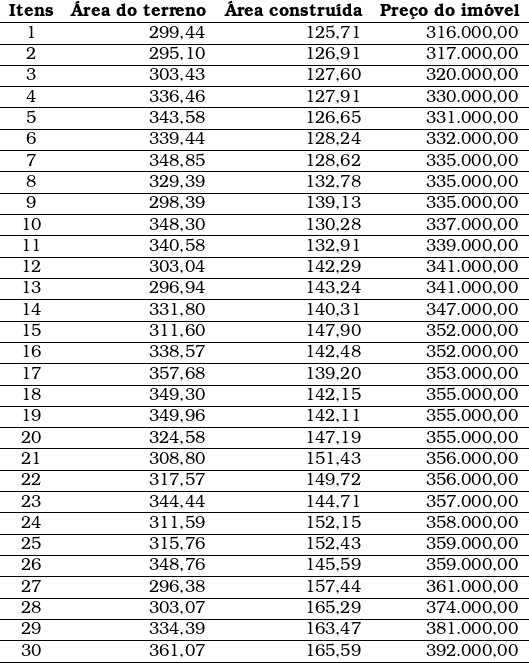
Os coeficientes calculados pela regressão foram:

 

 

Inserindo os coeficientes acima na equação do modelo linear generalizado, temos:

 

Essa equação nos informa que a cada alteração de uma unidade no eixo horizontal da variável x₁, serão acrescentadas 297,92 unidades no eixo vertical da variável dependente; e que a cada alteração de uma unidade no eixo horizontal da variável x₂, serão acrescentadas 1.438,66 unidades no eixo vertical da variável dependente.

E, também, que no ponto em que as variáveis independentes x₁ e x₂ são iguais a zero, o plano com todos os resultados possíveis interceptará o eixo vertical da variável dependente no ponto 46.137,10.

Reunidos, todos os possíveis resultados da equação acima assumem a figura de um plano, o qual pode ser visualizado no gráfico abaixo: 

 

 

Os resíduos, parcela não explicada pelas variáveis independentes, são calculados pela fórmula:

 

 

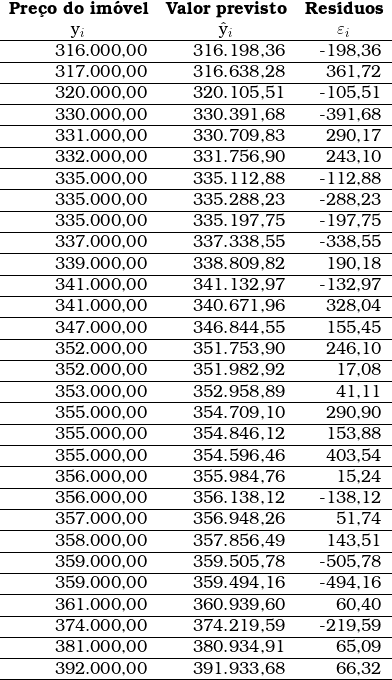
Os resíduos serão analisados em seção própria desta página.

 

 

 

Fontes:
ANTON, Howard; RORRES, Chris. Álbegra linear com aplicações [recurso eletrônico]. Porto Alegre: Bookman, 2012.
CASELLA, George; BERGER, Roger L. Inferência estatística. Tradução de Solange Aparecida Visconte. São Paulo: Cengage Learning, 2018.
CHARNET, Reinaldo; FREIRE, Clarice Azevedo de Luna; CHARNET, Eugênia M. Reginato; BONVINO, Heloísa.  Análise de modelos de regressão linear: com aplicações. 2. ed. Campinas,SP: Editora da Unicamp, 2008.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
______. Econometria: princípios, teoria e aplicações práticas; tradução de Cristina Yamagami; revisão técnica de Salvatore Benito Virgilito. São Paulo: Saraiva Educação, 2019.
HAIR JR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.
LATTIN, James; CARROLL, J. Douglas; GREEN, Paul E. Análise de dados multivariados. Tradução de Harue Avritscher. São Paulo: Cengage Learning, 2011.
LUNA, João Gil; OLINDA, Ricardo Alves. Introdução a modelos lineares. Campina Grande: EDUEPB, 2014.
MARINHO, Jefferson Luiz Alves. Avaliação de imóveis urbanos: análise dos pressupostos do modelo. São Paulo: Editora Leud, 2023.
NASSER JÚNIOR, Radegaz. Avaliação de bens: princípios básicos e aplicações. 3. ed. São Paulo: Editora Leud, 2019.
OLIVEIRA, Ana Maria de Biazzi Dias; GRANDISKI, Paulo. Métodos científicos e a engenharia de avaliações (com ênfase em inferência estatística). In:Engenharia de avaliações. v. 2. 2. ed. São Paulo: Livraria e Editora Universitária de Direito, 2014.