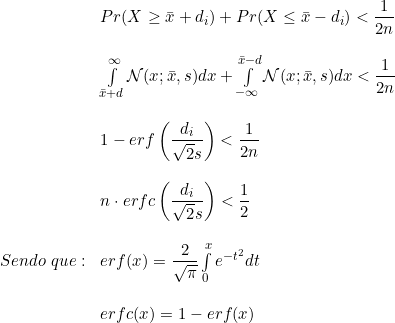Nesse procedimento, serão excluídos os itens cujo número de desvios-padrão ultrapassar os limites admissíveis. O tamanho da amostra determina qual é a amplitude da região de aceitação dos valores sob análise. Os valores máximo e mínimo do intervalo são calculados a partir do valores críticos de Chauvenet.

A equação para se calcular o valor d_i de cada item da amostra é:

$\qquad \qquad d_i = \left | \dfrac{x_i - \overline{x}}{s} \right | \indexspace \indexspace \begin{tabular}{llcl} Onde \colon & & & \\ & d_i & = & módulo do valor \textsl{d} de cada item da amostra \\ & x_i & = & item da amostra \\ & \overline{x} & = & média da amostra \\ & s & = & desvio-padrão da amostra \\ & & & \\ \end{tabular} \indexspace {Se d_i > d_{crítico}}, \quad então\ o\ elemento\ \textsl{i}\ é\ um\ ponto\ atípico\ (\ \textsl{outlier}\ ).$

O valor $ds_{crítico}$ é calculado pelas seguintes equações:

$\begin{array}{ll} & Pr ( X \ge \bar{x} + d_i) + Pr ( X \le \bar{x} - d_i) < \dfrac{1}{2n} \\ & \\ & \int\limits_{\bar{x} + d}^{\infty} \mathcal{N} (x ; \bar{x}, s) dx + \int\limits_{- \infty}^{\bar{x} - d} \mathcal{N} (x ; \bar{x}, s) dx < \dfrac{1}{2n} \\ & \\ & 1 - erf \left ( \dfrac{d_i}{\sqrt{2} s} \right ) < \dfrac{1}{2n} \\ & \\ & n \cdot erfc \left ( \dfrac{d_i}{\sqrt{2} s} \right ) < \dfrac{1}{2} \\ & \\ Sendo\ que:\ & erf(x) = \dfrac{2}{\sqrt{\pi}} \int\limits_{0}^{x} e^{- t^2} dt \\ & \\ & erfc(x) = 1- erf(x) \\ & \\ \end{array}$

Tabela de valores críticos de Chauvenet