Em Estatística, define-se média como sendo o valor central a partir do qual as medições se dispersam (SALSBURG, 2009, p. 29); o seu cálculo é simples, sendo a soma de todos os elementos dividida pelo número de elementos. Uma vez que a pesquisa feita no mercado revela que a variabilidade dos dados costuma ser a regra, raramente os dados observados se acomodarão à média calculada. Ainda sobre a média, pode-se dizer:
Existe outro tipo de numerozinho que não está ali cuja ausência pode ser igualmente prejudicial. É o que diz a faixa de variação ou seu desvio da média apresentada. Com frequência, uma média – seja aritmética ou mediana, especificada ou não especificada – é uma simplificação tão exagerada que não tem nenhuma utilidade. Não saber nada sobre um assunto muitas vezes é mais saudável do que saber o que não é verdadeiro, e saber pouco pode ser perigoso (Huff, 2016, p. 53).
Apesar de sua simplicidade, a aplicação da média pode trazer mais problemas do que soluções, levando a estimativas distorcidas. Consideremos uma série dados que, ao serem plotados, resultem no seguinte gráfico:
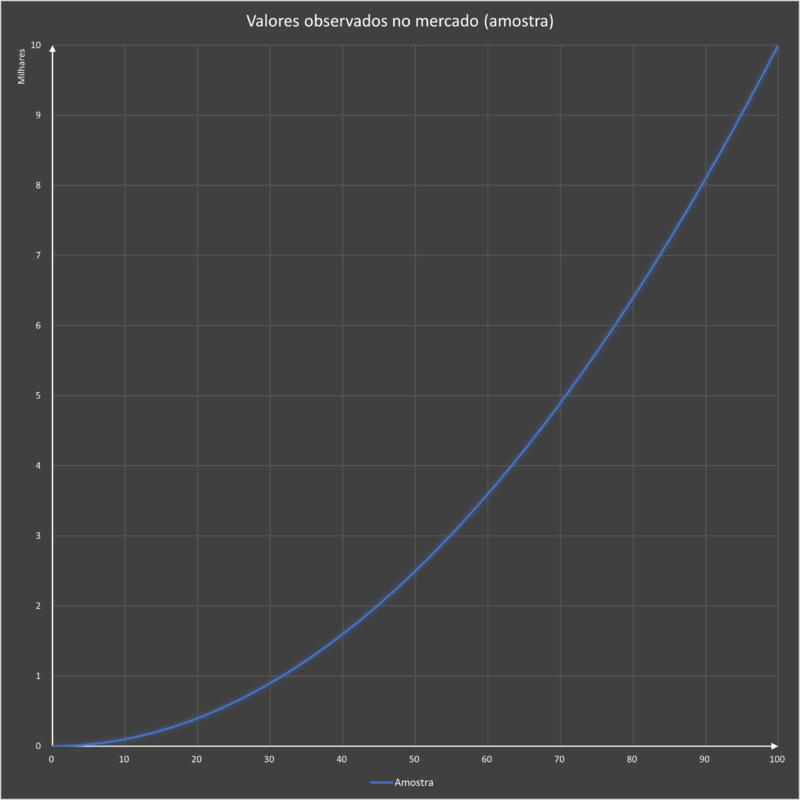
VALOR UNITÁRIO MÉDIO
Os resultados do modelo que utilizou o valor unitário médio podem ser ilustrados no gráfico abaixo:
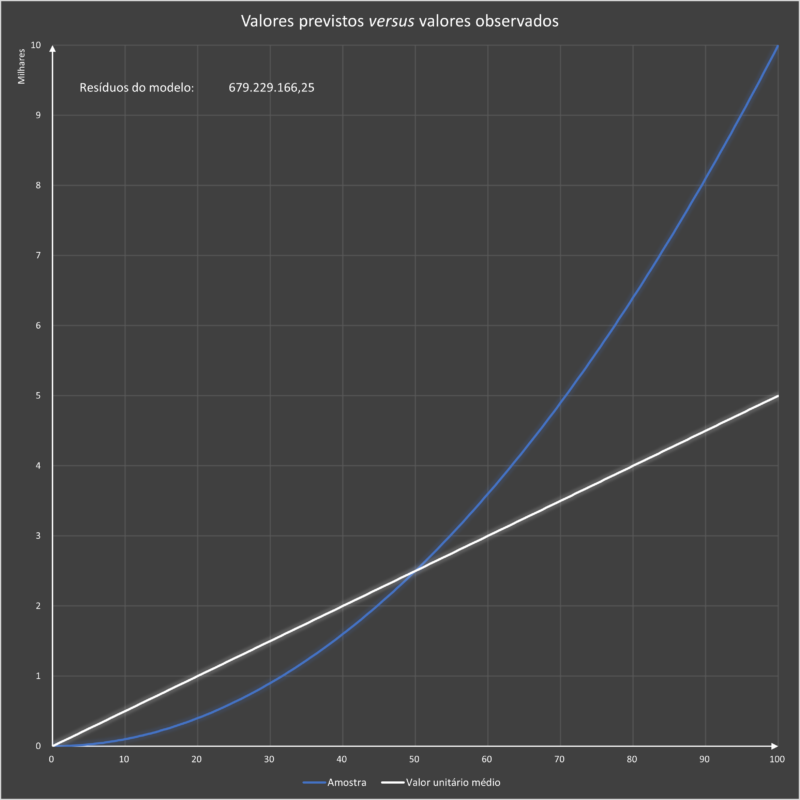
O modelo que utilizou o valor unitário médio gerou um resíduo correspondente a 679.229.166,25.
ANÁLISE DE DADOS POR MODELOS DE REGRESSÃO LINEAR SIMPLES (UMA VARIÁVEL INDEPENDENTE)
INTERSEÇÃO LIVRE
Prosseguindo com a comparação, os resultados do modelo de regressão linear simples com interseção livre foram:
| RESUMO DOS RESULTADOS | |||||
| Estatística de regressão | |||||
| R múltiplo | 96,79% | ||||
| R-Quadrado | 93,69% | ||||
| R-quadrado ajustado | 93,66% | ||||
| Erro padrão | 756,55 | ||||
| Observações | 201 | ||||
| ANOVA | |||||
| gl | SQ | MQ | F | F de significação | |
| Regressão | 1 | 1.691.750.000,00 | 1.691.750.000,00 | 2.955,67 | 0,000000% |
| Resíduo | 199 | 113.902.707,92 | 572.375,42 | ||
| Total | 200 | 1.805.652.707,92 | |||
| Coeficientes | Erro padrão | Stat t | valor-P | ||
| Interseção | -1.658,33 | 106,33 | -15,60 | 0,000000% | |
| x | 100,00 | 1,84 | 54,37 | 0,000000% | |
O modelo de análise de dados em um modelo de regressão linear simples com interseção livre gerou um resíduo correspondente a 113.902.707,92.
Esses resultados podem ser plotados no gráfico abaixo.
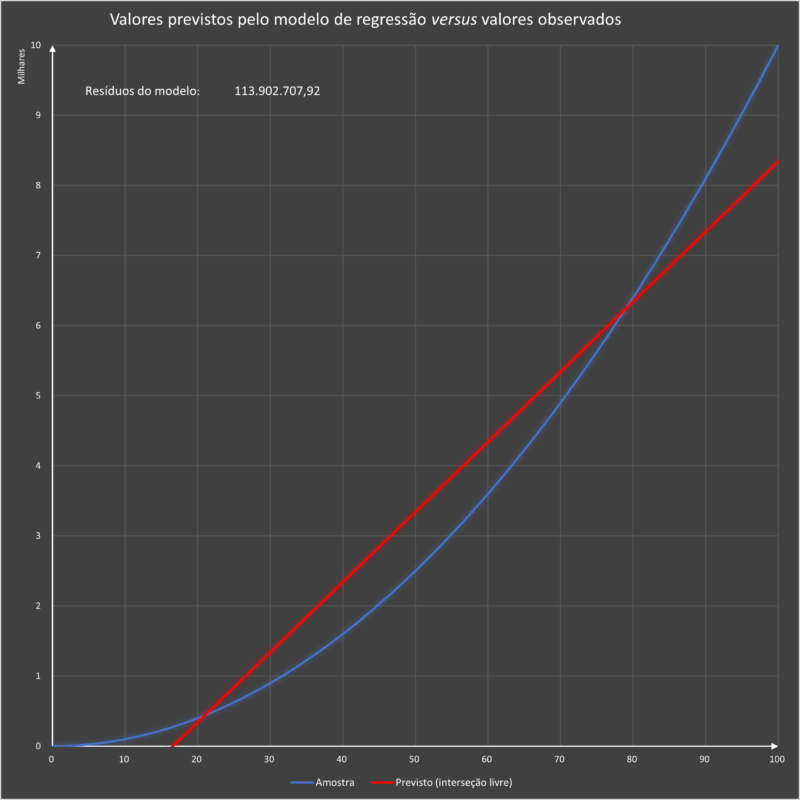
ANÁLISE DE DADOS POR MODELOS DE REGRESSÃO LINEAR SIMPLES (UMA VARIÁVEL INDEPENDENTE)
INTERSEÇÃO EM ZERO
Por sua vez, os resultados do modelo de regressão linear com interseção em zero foram:

O modelo de análise de dados em um modelo de regressão linear simples com interseção livre gerou um resíduo correspondente a 253.127.545,30.
Esses resultados podem ser plotados no gráfico abaixo.
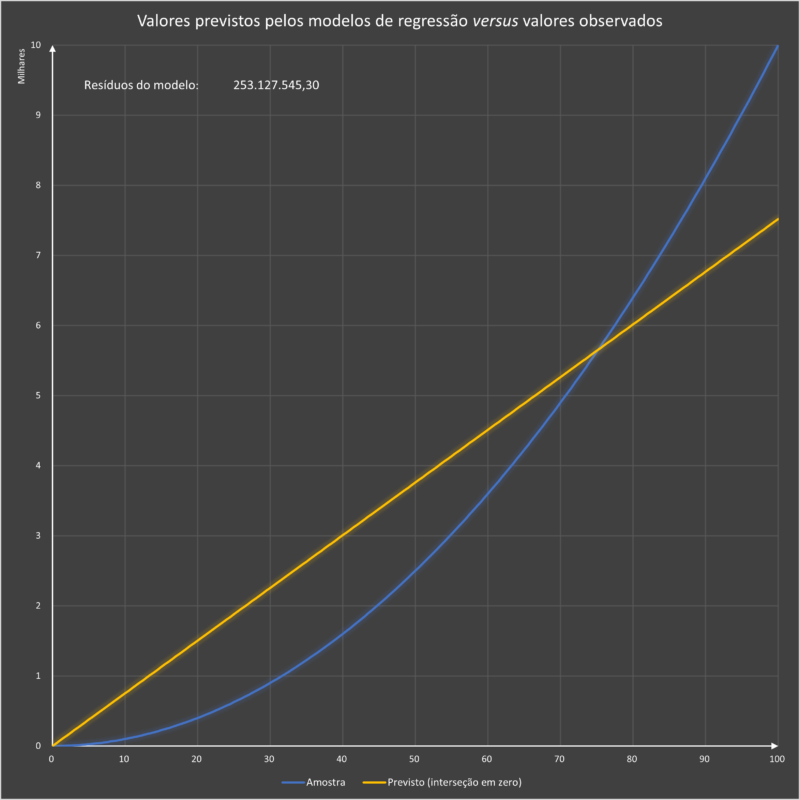
COMPARAÇÃO ENTRE OS DOIS MODELOS DE REGRESSÃO LINEAR
Plotagem dos resultados dos dois modelos de regressão linear simples: interseção livre e interseção em zero.
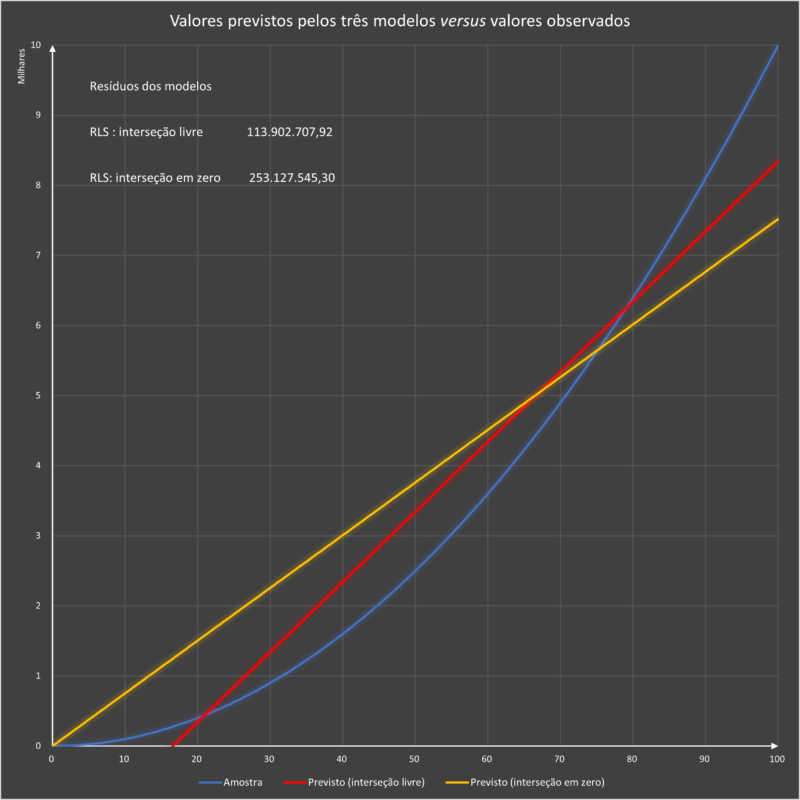
Pode-se observar que o modelo de regressão linear com interseção livre se ajusta melhor à série de dados. Isso pode ser demonstrado matematicamente, pois a soma quadrática dos resíduos não explicados é a menor entre os três métodos.
COMPARAÇÃO ENTRE OS TRÊS MODELOS
VALOR UNITÁRIO MÉDIO, REGRESSÃO LINEAR SIMPLES: INTERSEÇÃO LIVRE E INTERSEÇÃO EM ZERO
E, por fim, visualizando os resultados dos três modelos, temos:
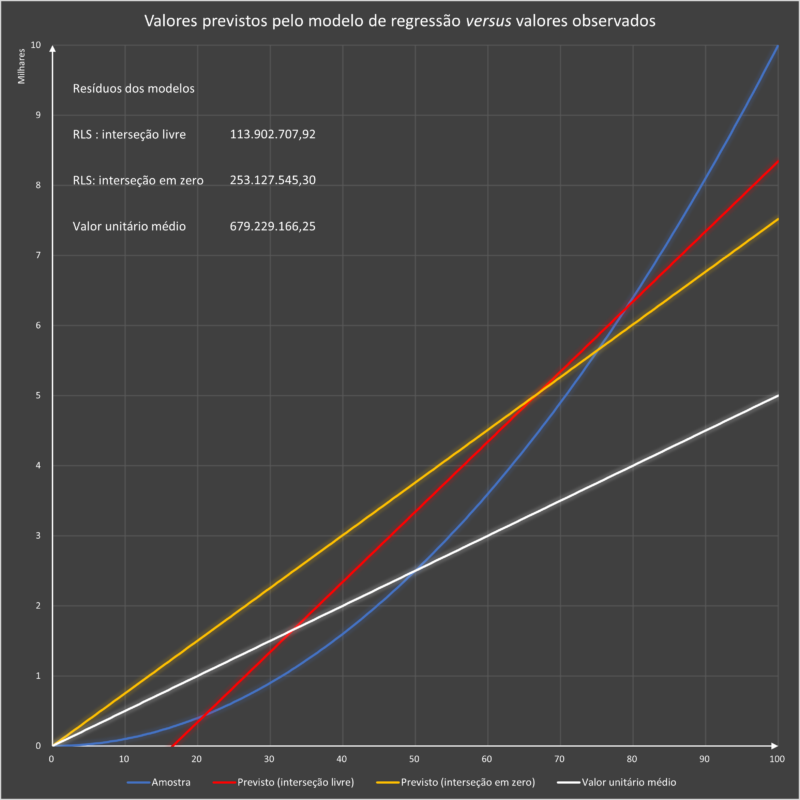
Entre os três modelos, aquele que melhor se adapta aos dados observados é o da regressão linear com interseção livre (linha vermelha) pois, observe-se, é o que produziu a menor soma quadrática de resíduos (113.902.707,92).
PROVIDÊNCIAS NECESSÁRIAS QUANDO SE UTILIZA A MÉDIA
Deve ser registrado, porém, que a média é um elemento que pode ser útil, desde que o modelo tenha passado pelos procedimentos de homogeneização e de saneamento da amostra.
O saneamento pode ser feito por um dos seguintes caminhos:
Deve-se, ainda, analisar se a homogeneização levou a resultados positivos, diminuindo a dispersão e, por consequência, o coeficiente de variação; ou, a resultados inesperados (heterogeneização do conjunto de dados). O coeficiente de variação ( cv ) é calculado pela seguinte fórmula: ![]() , onde:
, onde:
![]()
E, por fim, quando se utiliza a média como estimador, é necessário que se faça, no mínimo, o saneamento da amostra, o cálculo do intervalo de confiança de 80%, a análise do grau de precisão e do campo de arbítrio admissível.
Portanto, a opção pelo uso da média impõe ao avaliador que verifique se ele cumpriu todas as etapas previstas na norma técnica (NBR 14653).
Sugere-se, ainda, que o Avaliador identifique a mediana e a moda em seu conjunto de dados, pois esses números podem ser tão, ou até mais, úteis do que a simples média (MATTHEWS, 2017, p.231).
Fontes:
HUFF, Darrell. Como mentir com estatística. Tradutor Bruno Casotti. Rio de Janeiro: Intrínseca, 2016.
MATTHEWS, Roberto. As leis do acaso: como a probabilidade pode nos ajudar a compreender a incerteza. Tradução de George Schlezinger. Revisão técnica de Samuel Jurkiewicz. Rio de Janeiro: Zahar, 2017.
SALSBURG, David. Uma senhora toma chá: como a estatística revolucionou a ciência no século XX. Tradução de José Maurício Gradel. Revisão técnica de Suzana Herculano-Houzel. Rio de Janeiro: Zahar, 2009.

