Ensaio F de Snedecor

Teste de nível de significância máximo para a rejeição da hipótese nula do modelo (ensaio F de Snedecor)

 

Nesse ponto, devemos observar as diretrizes contidas na NBR 14653-2:2011. Avaliação de bens. Parte 2: Imóveis urbanos. Item 9.2.1, tabela 1, item 6.

Esse teste considera a probabilidade máxima admissível de se rejeitar a hipótese nula quando a mesma é verdadeira (erro tipo I), ou seja, a chance de o teste exibir significância estatística quando na verdade essa significância não está presente – o caso de um faso positivo (HAIR et al., 2009, p. 27).

Os testes abaixo se referem ao exemplo apresentado nesta página na seção Solução matricial I.

 

 

 

O nível de significância máximo admitido na norma é de 5% (cinco por cento), para o grau de fundamentação I.

Assim, para se rejeitar a hipótese de não haver regressão ao nível 5%, é necessário que F_c seja superior a F_{(0,05;k;n-k-1)}, que se encontra tabelado por Fisher; em caso contrário há indícios de que pelo menos uma das variáveis pode ser considerada importante para explicar a formação de preços. (DANTAS, 1998, p. 157)

 

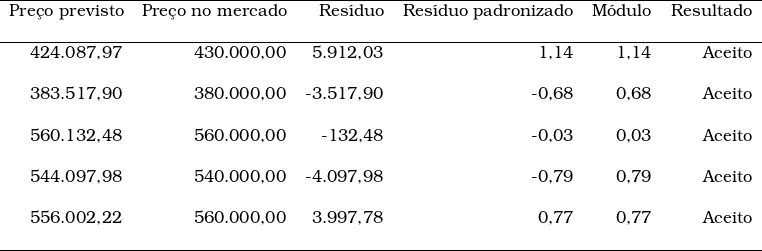
Os resultados calculados pela regressão foram:

 

 

 

 

 

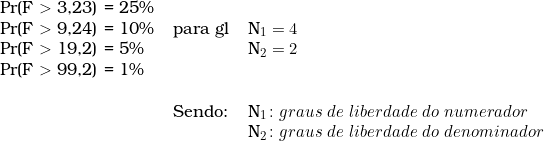
Os resultados indicam que a regressão atingiu o ponto 567,19 na estatística F, portanto superior a 19,2, que é o valor crítico fixado com base nos graus de liberdade do modelo, em um nível de significância máximo de 5% (cinco por cento). Pode-se, pois, rejeitar a hipótese nula do modelo.

Os pontos percentuais superiores estão disponíveis para consulta nesta página na seção Distribuição F, e foram confrontados com aqueles apresentados por Gujarati (2006, p. 778).

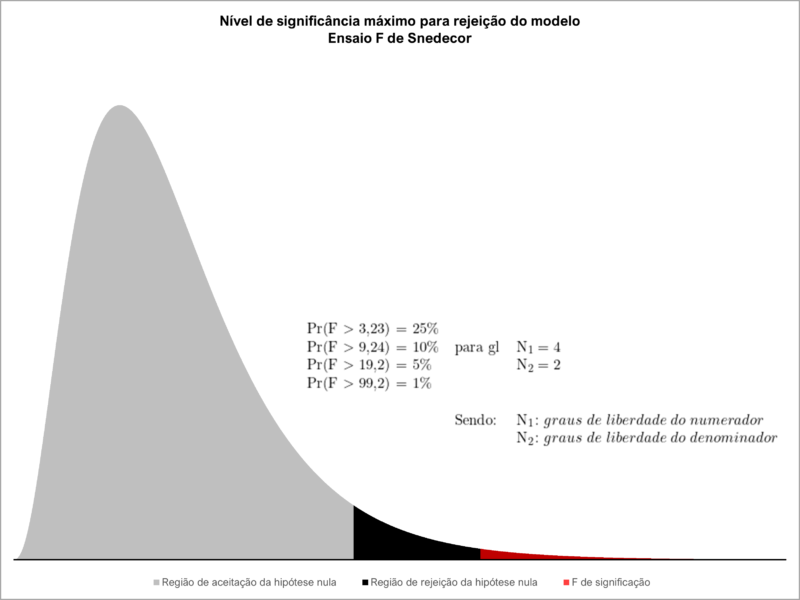
O resultado do teste F de Snedecor (ou ensaio F de Snedecor) pode ser demonstrado visualmente no gráfico abaixo:

 

 

 

Análise de normalidade

 

 

Fontes:
DANTAS, Rubens Alves. Engenharia de avaliações: uma introdução à metodologia científica. São Paulo: Pini, 1998.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
HAIR JR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.
LATTIN, James; CARROLL, J. Douglas; GREEN, Paul E. Análise de dados multivariados. Tradução de Harue Avritscher. São Paulo: Cengage Learning, 2011.