Análise de normalidade | Oficial de Justiça Avaliador

TESTES DE NÍVEL DE SIGNIFICÂNCIA (ERRO TIPO I)

Os testes abaixo se referem ao exemplo apresentado nesta página na seção Solução matricial I.

ANÁLISE DE NORMALIDADE DOS RESÍDUOS

Teste de nível de significância de cada regressor

A estatística-t é calculada pela razão entre o coeficiente regressor e o seu respectivo erro padrão:

$\begin{tabular}{p{3cm}p{5cm}p{3cm}} Intercepto & = {79.138,55} \div\ {90.481,09} & = 0,874642 \\ Área do terreno & = {340,04} \div\ {318,69} & = 1,067017 \\ Área construída & = {1.943,49} \div\ {74,45} & = 26,105020 \\ \end{tabular}$

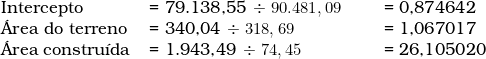
Nesse ponto, devemos observar as diretrizes contidas na NBR 14653-2:2011. Avaliação de bens. Parte 2: Imóveis urbanos. Item 9.2.1, tabela 1, item 5.

$\begin{tabular}{p{10cm}p{2cm}p{2cm}p{2cm}} \\ & \multicolumn{3}{c}{\textbf{Grau de fundamentação}} \\ \cline{1} \hline \multicolumn{1}{c}{\textbf{Descrição}} & \multicolumn{1}{c}{\textbf{III}} & \multicolumn{1}{c}{\textbf{II}} & \multicolumn{1}{c}{\textbf{I}} \\ \hline Nível de significância alfa (somatório do valor das duas caudas) máximo para a rejeição da hipótese nula de cada regressor (teste bicaudal) & \multicolumn{1}{c}{10\%} & \multicolumn{1}{c}{20\%} & \multicolumn{1}{c}{30\%} \\ \hline & & & \\ \end{tabular}$

O nível de significância máximo estabelecido na norma é de 30% (trinta por cento), para o grau de fundamentação I.

A amostra do exemplo acima contém 7 elementos. No modelo matemático de análise dessa amostra foram consideradas 2 (duas) variáveis independentes, quais sejam: área do terreno e área construída, além do intercepto (constante).

Nessa configuração, o valor crítico é dado por:

$\begin{tabular}{lcl} t_{(1\!-\! \alpha;n\!-\!k\!-\!1)}\ & = & \ limite\ na\ estatística-t\ de\ Student\ \\ \alpha\ & = & \textsl{ nível\ de\ significância} \\ 1 - \alpha\ & = & \textsl{ coeficiente}\ de\ significância\ \\ n\ & = & \ tamanho\ da\ amostra\ \\ k\ & = & \ variáveis\ independentes\ inseridas\ no\ modelo\ \end{tabular}$

Na configuração do exemplo, o valor crítico é 1,189567, conforme consta na tabela da distribuição-t de Student. Os resultados da regressão foram:

$\begin{tabular}{lrrr} \multicolumn{4}{l}{\textbf{Análise da variância (ANOVA)}} \\ \hline ~ & \textsl{Coeficientes} & \textsl{Erro padrão} & \textsl{Estatística-t} \\ \hline \textbf{Intercepto} & 79.138,55 & 90.481,09 & 0,874642 \\ \textbf{Área do terreno} & 340,04 & 318,69 & 1,067017 \\ \textbf{Área construída} & 1.943,49 & 74,45 & 26,105020 \\ \hline \end{tabular}$

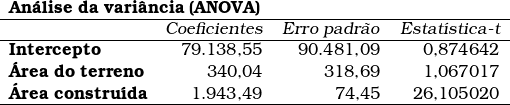
Portanto, em um nível de significância de 30% (trinta por cento), os coeficientes regressores do intercepto e da área do terreno se encontram na região de aceitação da hipótese nula, lembrando que nesse teste:

(1) $\begin{align*} H_0 \colon & \beta_k = 0 \\ H_1 \colon & \beta_k \neq 0 \end{align*}$

No caso, a probabilidade de que $\beta_0 e \beta_1 = 0$ é maior do que 30% (trinta por cento) e por isso, com relação a esses coeficientes, a hipótese nula não pode ser rejeitada.

A situação pode ser demonstrada visualmente nos dois primeiros gráficos abaixo; observe-se que o primeiro e o segundo coeficientes regressores se encontram na região de aceitação da hipótese nula (GUJARATI, 2006, p. 105).

Intercepto

O intercepto se encontra na área de aceitação da hipótese nula; portanto, em relação ao intercepto não se pode rejeitar a hipótese nula.

Desse modo, seguindo as orientações contidas nas normas NBR 14653-2:2011 e 14653-3:2019, o intercepto não é estatisticamente útil para o modelo adotado.

Coeficiente da variável independente: Área do terreno ( x₁ )

O coeficiente regressor relativo à variável independente área do terreno também se encontra na área de aceitação da hipótese nula; portanto, em relação ao seu respectivo coeficiente regressor, não se pode rejeitar a hipótese nula.

Desse modo, seguindo as orientações contidas nas normas NBR 14653-2:2011 e 14653-3:2019, a variável independente área do terreno não é estatisticamente útil para o modelo adotado.

Coeficiente da variável independente: Área construída ( x₂ )

O coeficiente regressor relativo à variável independente área construída se encontra na área de rejeição da hipótese nula; portanto, em relação ao seu respectivo coeficiente regressor, pode-se rejeitar a hipótese nula.

Desse modo, seguindo a orientação contida nas normas NBR 14653–2:2011 e 14653-3:2019, afirma-se que variável independente área construída é estatisticamente útil para o modelo adotado.

Teste de nível de significância do modelo (ensaio F de Snedecor)

Nesse ponto, devemos observar as diretrizes contidas na NBR 14653-2:2011. Avaliação de bens. Parte 2: Imóveis urbanos. Item 9.2.1, tabela 1, item 6.

$\begin{tabular}{p{10cm}p{2cm}p{2cm}p{2cm}} \\ & \multicolumn{3}{c}{\textbf{Grau de fundamentação}} \\ \cline{1} \hline \multicolumn{1}{c}{\textbf{Descrição}} & \multicolumn{1}{c}{\textbf{III}} & \multicolumn{1}{c}{\textbf{II}} & \multicolumn{1}{c}{\textbf{I}} \\ \hline Nível de significância máximo admitido para a rejeição da hipótese nula do modelo através do teste F de Snedecor & \multicolumn{1}{c}{1\%} & \multicolumn{1}{c}{2\%} & \multicolumn{1}{c}{5\%} \\ \hline & & & \\ \end{tabular}$

O nível de significância máximo admitido na norma é de 5% (cinco por cento), para o grau de fundamentação I.

$\begin{tabular}{lcrrrr} \multicolumn{6}{l}{\textbf{Análise da variância (ANOVA)}} \\ \hline ~ & \textsl{gl} & \textsl{SQ} & \textsl{MQ} & \textsl{F} & \textsl{F de significação} \\ \textbf{Regressão} & 2 & 30.663.305.631,70 & 15.331.652.815,85 & \textbf{567,19} & 0,001235\% \\ \textbf{Residual} & 4 & 108.122.939,72 & 27.030.734,93 & ~ & \\ \textbf{Total} & 6 & 30.771.428.571,43 & ~ & ~ & \\ \hline \end{tabular}$

$F = \dfrac{SQReg/k}{SQRes/(n\!-\!k\!-\!1)} = \dfrac{30.663.305.631,70/2}{108.122.939,72/4} = \textbf{567,19}$

$\begin{tabular}{lll} Pr(F \textgreater\ 3,23) = 25\% & & \\ Pr(F \textgreater\ 9,24) = 10\% & para gl & N_1 = 4 \\ Pr(F \textgreater\ 19,2) = 5\% & & N_2 = 2 \\ Pr(F \textgreater\ 99,2) = 1\% & & \\ \\ & Sendo: & N_1 \colon graus\ de\ liberdade\ do\ numerador\ \\ & & N_2 \colon graus\ de\ liberdade\ do\ denominador\ \\ \end{tabular}$

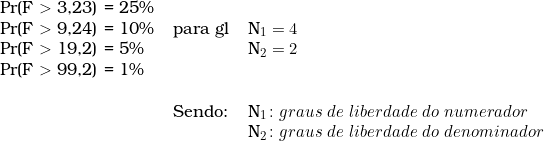
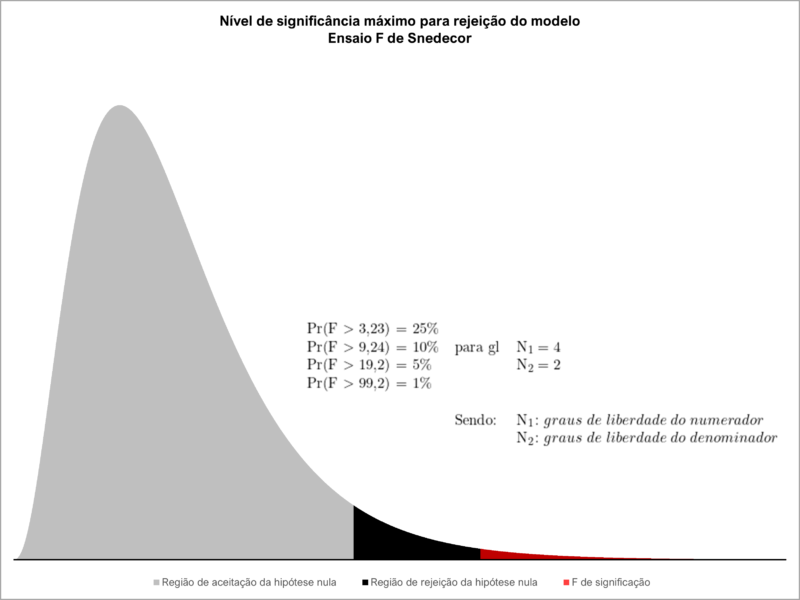
Os resultados indicam que a regressão atingiu o ponto 567,19 na estatística F, portanto superior a 19,2, que é o limite crítico fixado com base nos graus de liberdade do modelo, em um nível de significância máximo de 5% (cinco por cento). Pode-se, pois, rejeitar a hipótese nula do modelo.

Os pontos percentuais superiores estão disponíveis para consulta na página: Distribuição F.

O resultado do teste F de Snedecor (ou ensaio F de Snedecor) pode ser demonstrado visualmente no gráfico abaixo:

Análise de normalidade

$\begin{tabular}{rrrrrr} \hline Preço previsto & Preço no mercado & Resíduo & Resíduo padronizado & Módulo & Resultado & ~ & ~ \\ \hline 424.087,97 & 430.000,00 & 5.912,03 & 1,14 & 1,14 & Aceito & ~ & ~ \\ 383.517,90 & 380.000,00 & -3.517,90 & -0,68 & 0,68 & Aceito & ~ & ~ \\ 560.132,48 & 560.000,00 & -132,48 & -0,03 & 0,03 & Aceito & ~ & ~ \\ 544.097,98 & 540.000,00 & -4.097,98 & -0,79 & 0,79 & Aceito & ~ & ~ \\ 556.002,22 & 560.000,00 & 3.997,78 & 0,77 & 0,77 & Aceito & ~ & ~ \\ \hline \end{tabular}$

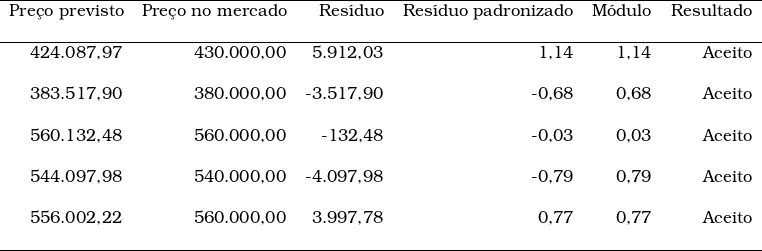
Fontes:
HAIR JR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.