Correlação III

Correlação estatisticamente insignificante

 

No conjunto de dados abaixo, a variável dependente y varia em função da variável independente x1; portanto, cada valor das linhas da primeira coluna está correlacionado ao respectivo valor da segunda coluna, porém não de modo exato.

 

\begin{tabular}{lr} \textbf{x} & \textbf{f(x)} \\ \hline 1 & 4,080 \\ \hline 2 & 4,090 \\ \hline 3 & 4,090 \\ \hline 4 & 4,090 \\ \hline 5 & 4,090 \\ \hline 6 & 4,090 \\ \hline 7 & 4,090 \\ \hline 8 & 4,090 \\ \hline 9 & 4,090 \\ \hline 10 & 4,090 \\ \hline 11 & 4,090 \\ \hline 12 & 4,090 \\ \hline 13 & 4,090 \\ \hline 14 & 4,090 \\ \hline 15 & 4,085 \\ \hline ~ & \\ Correlação & \textbf{0,199} \\ \hline \end{tabular}

 

 

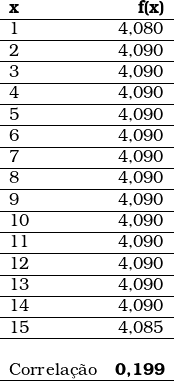
Os coeficientes regressores podem ser calculados pelas fórmulas já apresentadas; todavia, o conjunto de dados acima foi submetido à ferramenta de análise; os resultados da regressão linear foram:

\begin{tabular}{p{4cm}p{3cm}p{3cm}p{3cm}p{3cm}p{3cm}} \multicolumn{1}{l}{\textbf{ANOVA}} & ~ & ~ & ~ & ~ & \\ % comentários % ~ & gl & SQ & MQ & F & F de significação \\ \hline \multicolumn{1}{l}{Regressão} & 1 & 4,37E-06 & 4,37E-06 & 0,538 & 47,61\% \\ \hline \multicolumn{1}{l}{Resíduo} & 13 & 1,06E-04 & 8,12E-06 & ~ & \\ \hline \multicolumn{1}{l}{Total} & 14 & 1,10E-04 & 0,00E+00 & ~ & \\ \hline ~ & ~ & ~ & ~ & ~ & \\ ~ & Coeficientes & Erro padrão & Stat t & valor-P & \\ \hline \multicolumn{1}{l}{Interseção} & 4,088000 & 0,002 & 2.639,447 & 0,00\% & \\ \hline \multicolumn{1}{l}{x} & 0,000125 & 0,000170346 & 0,734 & 47,61\% & \\ \hline \end{tabular}

 

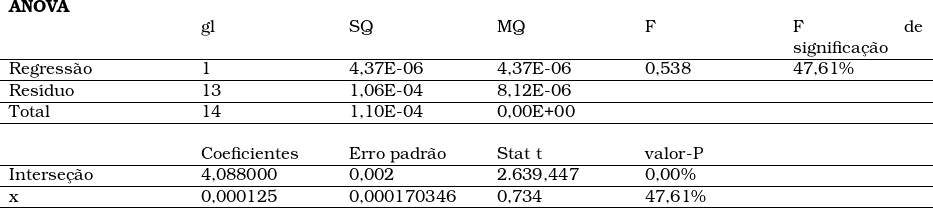
O valor-P que consta nos resultados da análise de variância se refere ao teste bicaudal realizado para o cálculo do nível de significância para a rejeição hipótese nula em relação a cada coeficiente regressor. Essa previsão consta nas normas técnicas NBR 14653-2:2011 (item 9.2.1; tabela 1, item 5) e NBR 14653-3:2019 (item 9.3.1; tabela 2, item 5). O nível máximo de significância aceito por essas normas é de 30% (trinta por cento) para o grau de fundamentação I.

Portanto, em um nível de significância de 47,61% não podemos rejeitar a hipótese nula, isso equivale a dizer que a probabilidade de que o coeficiente regressor da variável independente seja  0,00 (zero) é maior do que 30% (trinta por cento).

A situação pode ser demonstrada visualmente no gráfico abaixo; observe-se que o coeficiente regressor se encontra na área de não rejeição da hipótese nula.

 

 

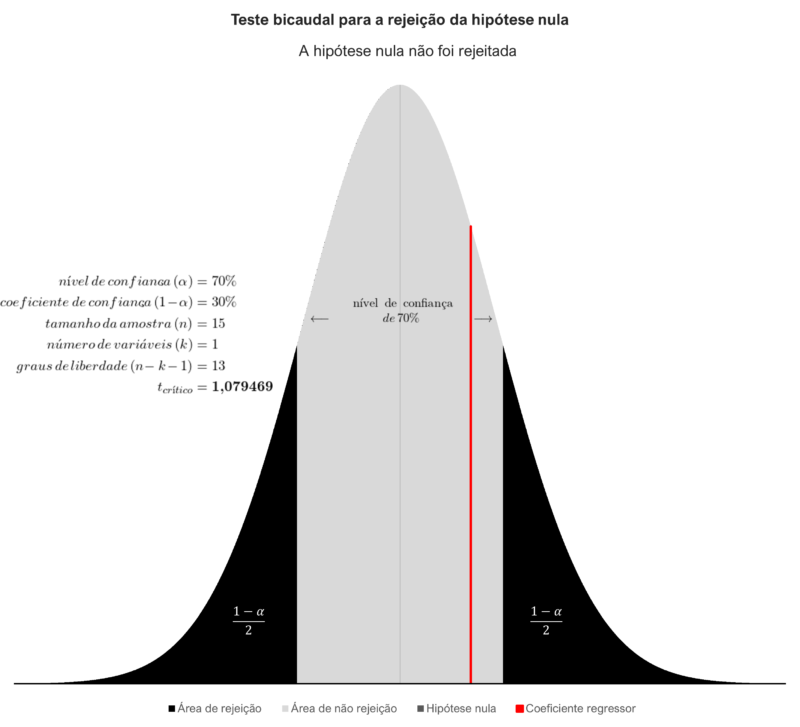
No âmbito do tratamento de dados por modelo de regressão linear essa é uma das principais consequências de uma correlação estatisticamente insignificante entre as variáveis inseridas no modelo.

Os resultados previstos (variável dependente) pela regressão em relação à variável independente podem ser demonstrados visualmente no seguinte gráfico:

 

 

 

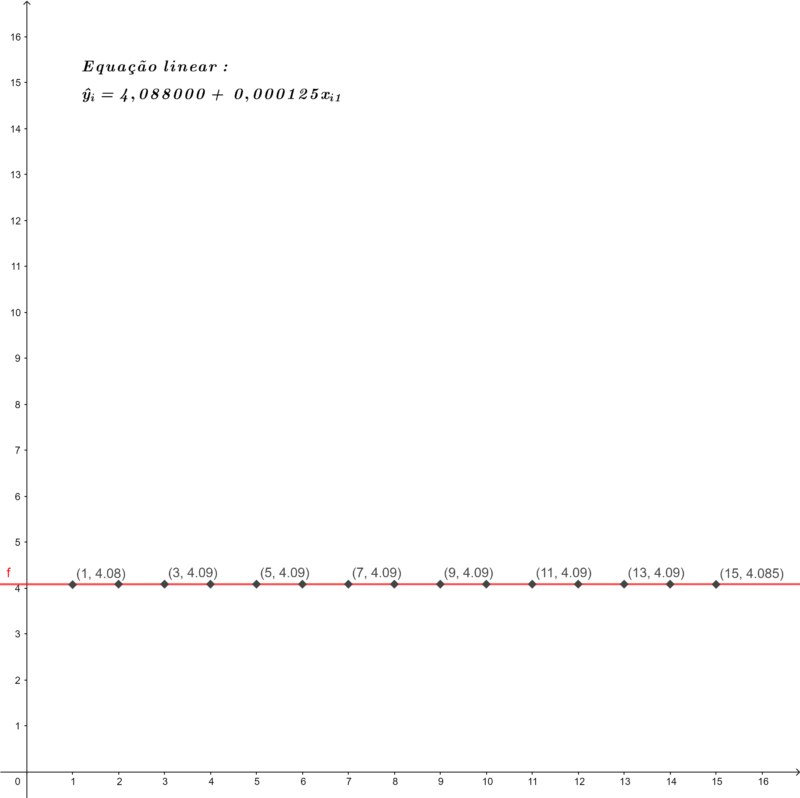
Fontes:
CASELLA, George; BERGER, Roger L. Inferência estatística. Tradução de Solange Aparecida Visconte. São Paulo: Cengage Learning, 2018.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
HAIR JR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.