Relação de dependência entre duas variáveis
O pesquisador, diante de variáveis dependentes de uma natureza métrica ou não-métrica, tem à disposição diversos métodos de dependência para ajudá-lo no processo de relacionar variáveis independentes com dependentes. Dada a natureza multivariada desses métodos, todas as técnicas de dependência acomodam múltiplas variáveis independentes e também permitem múltiplas variáveis dependentes em certas situações. Assim, o pesquisador tem um conjunto de técnicas que devem viabilizar a análise de praticamente qualquer tipo de questão de pesquisa que envolva uma relação de dependência. Elas também fornecem a oportunidade de se ter não apenas maior capacidade de previsão, mas uma explicação aprimorada da relação da variável dependente com as independentes. A explicação se torna cada vez mais importante à medida que as questões da pesquisa começam a abordar tópicos sobre como se dá a relação entre variáveis dependentes e independentes (HAIR JR et al., 2009, p. 147).
Conceitos principais
Coeficiente de correlação (r) coeficiente que indica a força da associação entre quaisquer duas variáveis métricas. O sinal ( + ou – ) indica a direção da relação. O valor pode variar de -1 a +1, onde +1 indica uma perfeita relação positiva, 0 indica relação nenhuma, e -1, uma perfeita relação negativa ou reversa (quando uma variável se torna maior, a outra fica menor) (ibidem, p. 150).
Coeficiente de correlação parcial. Valor que mede a força da relação entre a variável dependente ou critério e uma única variável independente quando os efeitos das demais variáveis independentes no modelo são mantidos constantes. Por exemplo, rY,X2,X1 mede a variação em Y associada à X2 quando o efeito de X1 em X2 e Y é mantido constante. Esse valor é usado em métodos de estimação de modelo de regressão com seleção sequencial de variáveis (p. exe., stepwise, adição forward ou eliminação backward) para identificar a variável independente com o maior poder preditivo incremental além das variáveis independentes já presentes no modelo de regressão (Ibidem, p. 150).
Coeficiente de determinação (R2). Medida da proporção da variância da variável dependente em torno de sua média que é explicada pelas variáveis independentes ou preditoras. O coeficiente pode variar entre 0 e 1. Se o modelo de regressão é propriamente aplicado e estimado, o pesquisador pode assumir que quanto maior o valor de R2, maior o poder de explicação da equação de regressão e, portanto, melhor a previsão da variável dependente (Ibidem, p. 150).
Coeficiente da regressão (bn). Valor numérico da estimativa do parâmetro diretamente associado com uma variável independente; por exemplo, no modelo Y = b0 + b1x1, o valor b1 é o coeficiente de regressão para a variável X1. O coeficiente de regressão representaria o montante da variação dependente em relação a uma unidade de variação na variável independente. No modelo preditor múltiplo (por exemplo, Y = b0 + b1x1 + b2x2), os coeficientes de regressão são coeficientes parciais, pois cada um considera não apenas as relações entre Y e X1 e entre Y e X2, mas também entre X1 e X2. O coeficiente não é limitado nos valores, já que é baseado tanto no grau de associação quanto nas unidades de escala da variável independente. Por exemplo, duas variáveis com a mesma associação a Y teriam coeficientes diferentes se uma variável independente fosse medida em uma escala de 7 pontos e outra fosse baseada em uma escala de 100 pontos (Ibidem, p. 150-151).
Intercepto (b0). Valor no eixo Y (eixo da variável dependente) onde a reta definida pela equação de regressão Y = b0 + b1X1 cruza o eixo. É descrito pelo termo constante b0 na equação de regressão. Além de seu papel na previsão, o intercepto pode ter uma interpretação gerencial. Se a completa ausência da variável independente tem significado, então o intercepto representa essa quantia. Por exemplo, quando se estimam vendas a partir de investimentos ocorridos em anúncios, o intercepto representa o nível de vendas esperadas se o anúncio for eliminado. Contudo, em muitos casos, a constante tem apenas valor preditivo, porque não há situação na qual todas as variáveis independentes estejam ausentes. Um exemplo é prever a preferência sobre um produto com base em atitudes de consumidores. Todos os indivíduos têm algum nível de atitude, e assim o intercepto não tem uso gerencial, mas ainda auxilia na previsão (Ibidem, p. 151).
No âmbito deste trabalho, restrito à avaliação patrimonial de bens e direitos, nossa pesquisa se limitará à relação de dependência entre uma ou múltiplas variáveis independentes e uma única variável dependente; somente as variáveis métricas, ou seja, aquelas cuja correlação pode ser mensurada, serão incluídas nos modelos de análise.
A correlação entre as variáveis independentes com a variável dependente será traduzida em uma equação linear; o modelo mais simples para explicar a correlação entre essas variáveis é:
![]()
Em análise de dados multivariados por meio da técnica da regressão linear, usam-se os símbolos:
![]()
Onde:
β0 = valor constante, ponto em que a reta intercepta o eixo vertical y; ponto conhecido como intercepto ou interseção.
β1 = coeficiente calculado pela regressão que dimensiona o impacto que a variável independente x1 causa na variável dependente y
No conjunto de dados abaixo, a variável dependente y varia em função da variável independente x; portanto, o valor de cada uma das linhas da primeira coluna está correlacionado ao respectivo valor na segunda coluna.
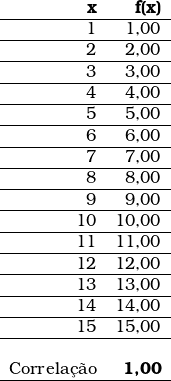
Se a correlação entre esses dois pontos for perfeita ( + 1 ou – 1 ), então esse conjunto de pontos se ajustará perfeitamente a uma reta.
A equação que explica a correlação entre os i pares de elementos do conjunto de variáveis do conjunto acima é:
![]()
O gráfico abaixo, gerado com o auxílio da ferramenta Geogebra, demonstra visualmente essa correlação perfeita positiva ( + 1 ) entre os valores da variável independente x e os valores da variável dependente y.
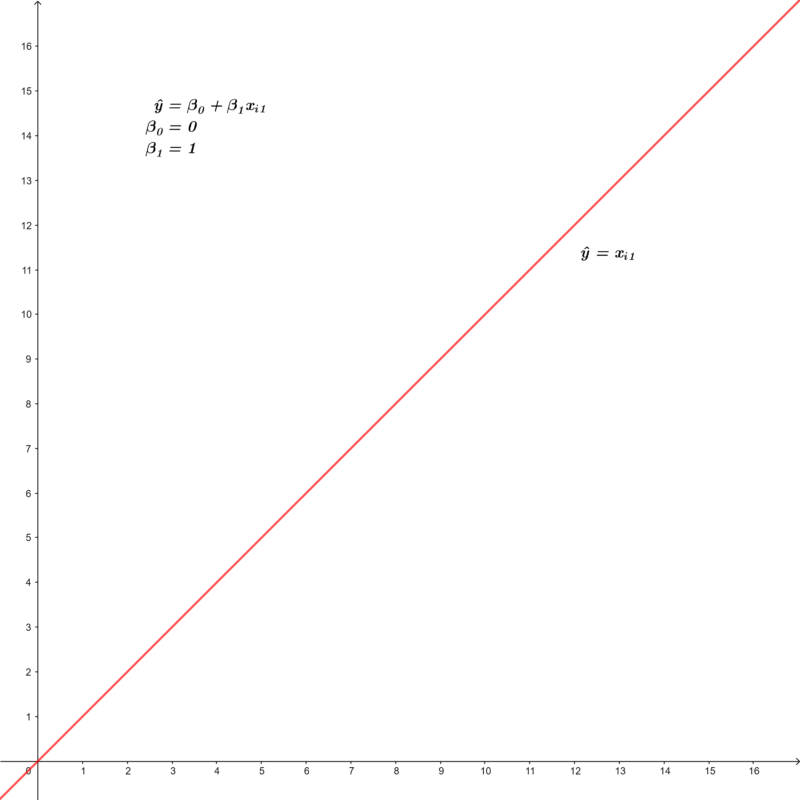
Um exemplo de correlação perfeita negativa ( – 1 ) é:
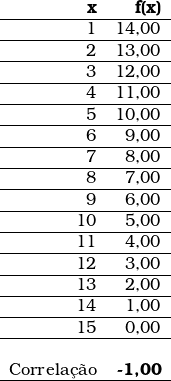
A correlação entre as duas variáveis também é perfeita, porém ela é negativa; vale dizer, conforme os valores da variável independente x aumentam, os valores da variável dependente y diminuem. Ainda assim, esse conjunto de pontos também se ajusta perfeitamente a uma reta.
A equação que explica a correlação entre essas duas variáveis é:
![]()
O gráfico abaixo demonstra visualmente essa correlação negativa.
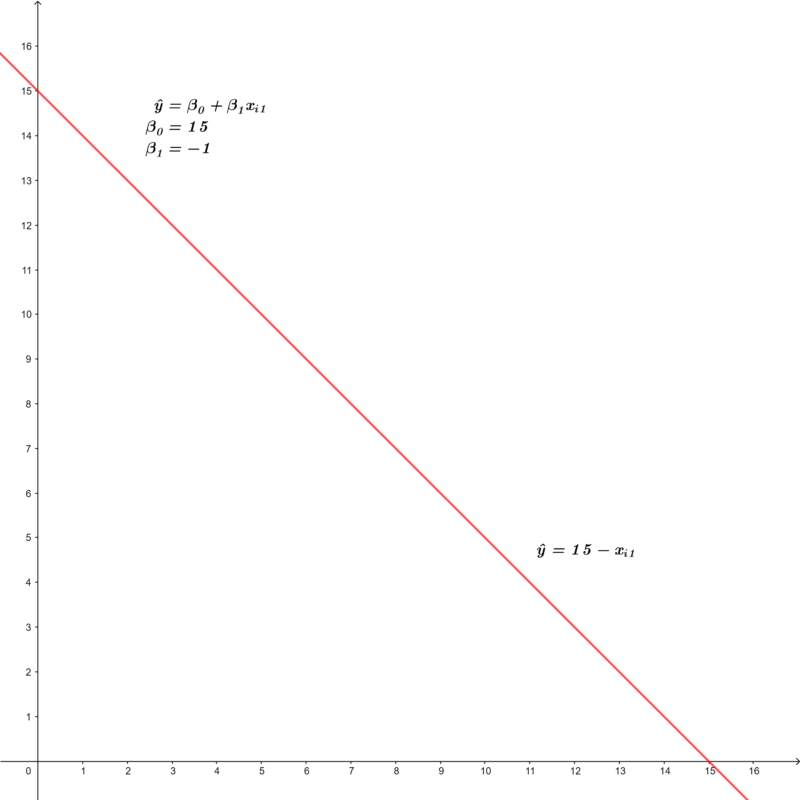
E, por fim, caso não exista qualquer relação de dependência entre as variáveis, o coeficiente de correlação é igual a 0,00 (zero):
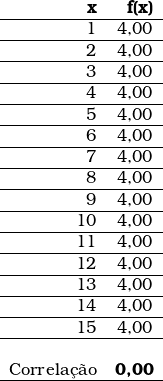
Observa-se que as alterações feitas na variável independente ( x1 ) não causam qualquer impacto na variável dependente ( y ).
A equação que traduz essa situação é:
![]()
Sendo:
![]()
Essa situação pode ser demonstrada visualmente no gráfico abaixo:
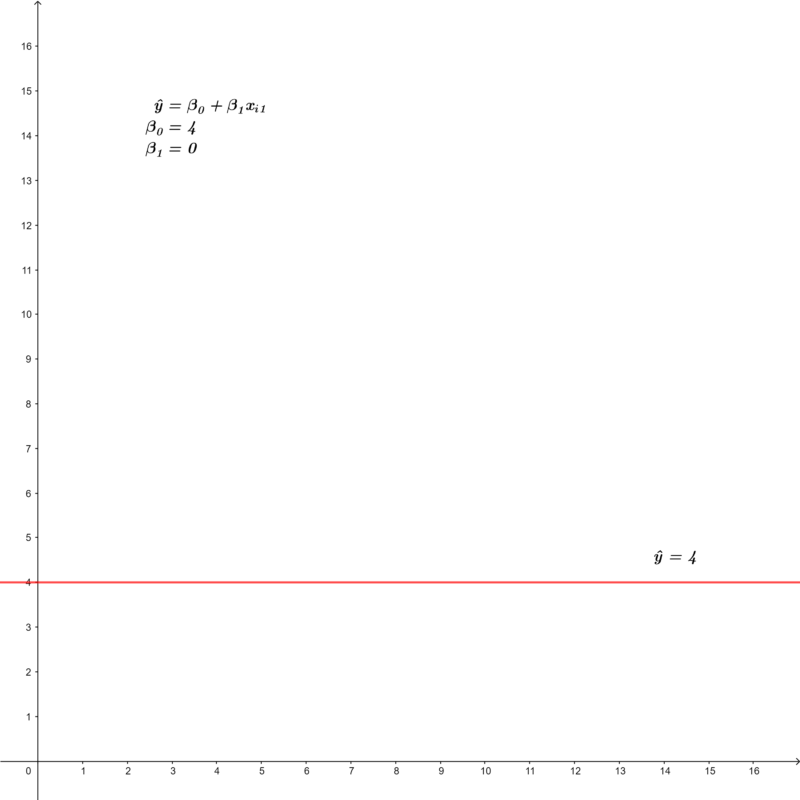
Cálculo do coeficiente de correlação
A correlação pode ser calculada com o auxílio da seguinte fórmula:
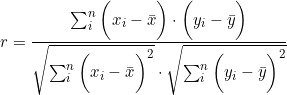
No programa Excel®, a correlação entre duas variáveis é calculada através da função CORREL. ou, no caso de múltiplas variáveis, através da ferramenta de análise de dados “Correlação”; essa ferramenta depende de habilitação no sistema.
Para a interpretação dos resultados, podemos considerar a tabela apresentada por González (2015, p. 69):
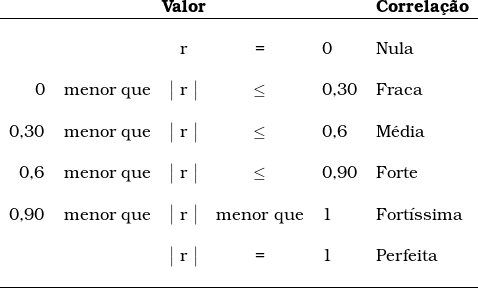
Fontes:
GEOGEBRA. Disponível em: https://www.geogebra.org Acesso em: 27 out. 2022.
GONZÁLEZ, Marco Aurélio Stumpf. Avaliação de imóveis: dos métodos clássicos às redes neurais. Saarbrücken, Alemanha: 2015.
HAIR JR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.

