SOLUÇÃO MATRICIAL PARA UM SISTEMA LINEAR
Consideremos o seguinte sistema linear:
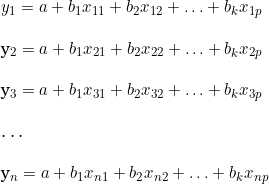
A notação matricial do sistema linear apresentado acima é:

Conforme Charnet (2008, p. 175), o vetor ![]() é composto pelas diferenças entre cada valor de y e o correspondente valor dado por uma função, ou seja:
é composto pelas diferenças entre cada valor de y e o correspondente valor dado por uma função, ou seja:
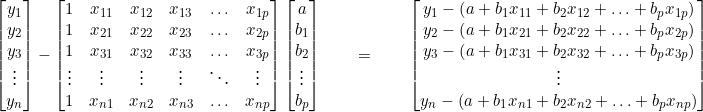 .
.
(1) ![Rendered by QuickLaTeX.com \begin{align*} \sum_{i=1}^n \left[ y_i - \left( a + b_1 x_{i1} + b_2 x_{i2} + \ldots + b_p x_{ip}\right)\right]^2 & = \left( y - Xb\right)'\left( y - Xb\right) \\ &= \left( y' - b'X'\right)\left( y - Xb\right) \\ &= y'y - y'Xb - b'X'y + b'X'Xb \end{align*}](https://oficialavaliador.com.br/wp-content/ql-cache/quicklatex.com-4268c2df4af253f526be9847fb989ab3_l3.png)
Derivando, simultaneamente, em termos de b, temos:
(2) 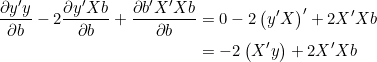
Denominando por ![]() o vetor que anula a derivada, podemos escrever:
o vetor que anula a derivada, podemos escrever:
(3) 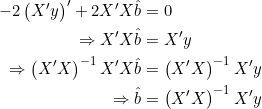
Portanto, supondo que a matriz ![]() seja inversível, temos:
seja inversível, temos:
![]()
Onde ![]() são os estimadores de quadrados mínimos; na regressão linear, esses são os coeficientes calculados associados a cada uma das k variáveis independentes, com o acréscimo do valor constante. Esses serão os resultados para melhor solução aproximada (LUNA; OLINDA, 2014, p. 64).
são os estimadores de quadrados mínimos; na regressão linear, esses são os coeficientes calculados associados a cada uma das k variáveis independentes, com o acréscimo do valor constante. Esses serão os resultados para melhor solução aproximada (LUNA; OLINDA, 2014, p. 64).
O erro padrão dos respectivos coeficientes regressores são calculados a partir dos elementos da diagonal principal da matriz ![]()
Portanto, os elementos da diagonal principal da matriz  são:
são: ![]() .
.
Então, calcula-se o desvio padrão estimado para cada um dos coeficientes regressores:
![]()
![]()
![]()
Sendo:
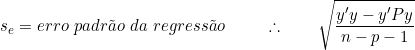
![]()
![]()
Fontes:
CASELLA, George; BERGER, Roger L. Inferência estatística. Tradução de Solange Aparecida Visconte. São Paulo: Cengage Learning, 2018.
CHARNET, Reinaldo; FREIRE, Clarice Azevedo de Luna; CHARNET, Eugênia M. Reginato; BONVINO, Heloísa. Análise de modelos de regressão linear: com aplicações. 2. ed. Campinas,SP: Editora da Unicamp, 2008.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
LATTIN, James; CARROLL, J. Douglas; GREEN, Paul E. Análise de dados multivariados. Tradução de Harue Avritscher. São Paulo: Cengage Learning, 2011.
LUNA, João Gil; OLINDA, Ricardo Alves. Introdução a modelos lineares. Campina Grande: EDUEPB, 2014.NASSER JÚNIOR, Radegas. Avaliação de bens: princípios básicos e aplicações. São Paulo: Editora Leud, 2019.
PINDYCK, Robert S.; RUBINFELD, Daniel L. Econometria: modelos e previsões. Rio de Janeiro: Elsevier, 2004.
WOOLDRIDGE, Jeffrey M. Introdução à econometria: uma abordagem moderna. Tradução da 6ª edição norte-americana. Tradução de Priscilla Rodrigues da Silva Lopes e Livia Marina Koeppl.

