Noções gerais

O conceito de homogeneização está presente no item 3.1.25 da NBR 14653-1:2019, nos seguintes termos:

3.1.25 homogeneização: tratamento dos preços observados, mediante a aplicação de transformações matemáticas que expressem em termos relativos, as diferenças entre os atributos dos dados de mercado e os do bem avaliando

A literatura apresenta o seguinte conceito: homogeneizar: 1. tornar(-se) homogêneo, semelhante a; igualar(-se) (HOUAISS, 2001)

Por sua vez, o conceito de tratamento de dados está presente no item 3.1.44 da mesma norma técnica, nos seguintes termos:

3.1.44 tratamento de dados: aplicação de operações que expressem, em termos relativos, as diferenças de atributos entre os dados de mercado e os do bem avaliando

Sobre a necessidade de se fazer a homogeneização da amostra, pode-se afirmar que:

Após a coleta dos elementos que servirão de base para a avaliação, o avaliador geralmente está diante de uma amostra formada por imóveis com características heterogêneas, tornando-se imprescindível a homogeneização dos dados em relação ao bem avaliando, ou a um paradigma adotado, para a utilização adequada do método comparativo. Nesta etapa são retiradas as vantagens ou desvantagens existentes nos dados de referência em relação ao bem avaliando ou a um paradigma adotado. Para isto devem-se utilizar as ferramentas de inferência estatística, através da busca de modelos explicativos do mercado imobiliário. (DANTAS, 1998, p. 16)

 

 

Homogeneização com um fator de ajuste

Aceitando que existe uma relação fixa entre o imóvel da amostra e o paradigma, de tal modo que:

\dfrac{paradigma}{f_p} = \dfrac{imóvel}{f_i} \quad \therefore \quad paradigma \quad = \quad \dfrac{imóvel \cdot f_pa}{f_b}

 

O paradigma, por ser o referencial, está associado ao fator 1,00, ou 100% (cem por cento); por hipótese, se o terreno da amostra for úmido, pela escala de Thofehrn se aplica o fator 0,80 (oitenta centésimos), então:

\dfrac{paradigma}{1,00} = \dfrac{imóvel}{0,80} \quad \therefore \quad paradigma \quad = \quad \dfrac{imóvel \cdot 1,00}{0,80}

 

Se o imóvel da amostra (dado coletado no mercado) está exposto à venda pelo valor de R$456,78 por metro quadrado, então:

\textbf{paradigma} = \dfrac{imóvel \cdot 1,00}{0,80} \quad \therefore \quad \dfrac{R\$\ 456,78 \cdot 1,00}{0,80} \quad \therefore \quad R\$\ 570,98\

 

Deve ser observado que, na fase de homogeneização, o fator relacionado ao imóvel da amostra foi aplicado de modo invertido; portanto, o procedimento acima está de acordo com a doutrina consagrada na área de avaliações:

Quando a homogeneização é feita em relação a um paradigma, o resultado do tratamento estatístico fornece um valor unitário básico. Deve-se observar que, partindo-se do valor unitário básico, para a avaliação do objeto os fatores de homogeneização apresentados devem ser usados de forma invertida. Isto porque, se um TR tem uma vantagem em relação ao paradigma, esta vantagem deve ser retirada na fase de homogeneização; porém, conhecendo-se o valor unitário básico, se um terreno avaliando tem uma vantagem em relação ao paradigma, esta vantagem deve ser dada. É o raciocínio inverso. (DANTAS, 1998, p. 21, grifo nosso)

 

O valor do metro quadrado do paradigma, elemento meramente intermediário nos cálculos, servirá como base de cálculo sobre a qual incidirá o fator, ou os fatores, do imóvel avaliando.

Se, por hipótese, o imóvel avaliando for alagadiço, aplica-se o fator 0,70 da escala Thofehrn; então o valor homogeneizado será:

R\$\ 570,98 \cdot 0,70 = R\$\ 399,70

 

No exemplo acima, o valor unitário homogeneizado (R$399,70) foi inferior ao inicial (R$456,78) porque o imóvel avaliando possui uma desvantagem em relação ao imóvel da amostra.

 

Homogeneização com mais de um fator de ajuste

O procedimento segue a mesma dinâmica apresenta acima; todavia os fatores devem ser utilizados na forma de somatório.

Suponhamos que estas são as características do imóvel da amostra:

imóvel\ da\ amostra\ \begin{cases} terreno\ úmido\ (fator\ =\ 0,80) \\ \indexspace declive\ de\ 5\%\ (fator\ =\ 0,95) \end{cases}

 

O imóvel da amostra sofreu dois tipos de desvalorização: a primeira, de -0,20 (vinte centésimos negativos) em razão da consistência do solo; a segunda, de -0,05 (cinco centésimos negativos) em razão do declive (inclinação para os fundos).

Portanto, o somatório dos fatores é:

\begin{tabular}{lcl} & f_1 & = 0,80 \\ & f_2 & = 0,95 \\ & & \\ & & \\ Desse\ modo:\ & f & = [(0,80 - 1) + (0,95 - 1)] + 1 \qquad \therefore \qquad [-0,20 + (-0,05)] + 1 \qquad \therefore \quad 0,75 \\ \end{tabular}

 

Se o imóvel da amostra está exposto no mercado por R$325,78 o metro quadrado, então o valor paradigma é:

paradigma = \dfrac{R\$\ 325,78}{0,75} \qquad \therefore \qquad R\$\ 434,38

 

Agora, digamos que as características e fatores próprios do imóvel avaliando sejam:

terreno\ avaliando\ \begin{cases} terreno\ alagadiço\ (fator\ =\ 0,70) \\ \indexspace terreno\ em\ aclive\ acima\ de\ 20\%\ (fator\ =\ 0,85) \end{cases}

 

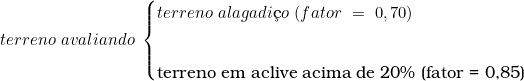
Neste exemplo, o terreno avaliando sofreu dois tipos de desvalorização: a primeira, de -0,30 (trinta centésimos negativos) em razão da consistência do solo; a segunda, de -0,15 (quinze  centésimos negativos) em razão do aclive  (caimento para a frente) acima de 20%.

Portanto, o somatório dos fatores é:

\begin{tabular}{lcl} & f_1 & = 0,70 \\ & f_2 & = 0,85 \\ & & \\ & & \\ Desse modo: & f & = [(0,70 - 1) + (0,85 - 1)] + 1 \qquad \therefore \qquad [-0,30 + (-0,15)] + 1 \qquad \therefore \qquad 0,55 \\ \end{tabular}

 

Por sua vez, o valor homogeneizado é:

R\$\ 434,38 \cdot 0,55 = R\$\ 238,90

 

No exemplo acima, o valor unitário homogeneizado (R$238,90) foi inferior ao inicial (R$325,78) porque o imóvel avaliando possui desvantagens em relação ao imóvel da amostra.

A equação do somatório de fatores pode ser generalizada:

Essa equação decorre da relação fixa existente entre os coeficientes k e seus respectivos fatores f :

 

\begin{tabular}{lll} \\ f & = & 1 + k \\ f - 1 & = & k \\ \end{tabular} \\ \vspace{1cm} \\ \underline{Portanto}: \\ \vspace{0.5cm} \\ \begin{tabular}{llllllllllll} \\ Somatório de fatores & = & f_1 & + & f_2 & + & f_3 & + & f_4 & + & f_5 & - n + 1 \\ Somatório de fatores & = & ( f_1 - 1 ) & + & (f_2 - 1) & + & (f_3 - 1) & + & (f_4 - 1) & + & (f_5 - 1) & + 1 \\ Somatório de fatores & = & k_1 & + & k_2 & + & k_3 & + & k_4 & + & k_5 & + 1 \\ Somatório de fatores & = & \multicolumn{10}{l}{Somatório de coeficientes + 1} \\ \end{tabular}

 

 

Após a homogeneização de todos os itens da amostra, passa-se para a fase do saneamento da amostra; por fim, a partir da média homogeneizada e saneada, passa-se para a fase de cálculo do intervalo de confiança, grau de precisão, grau de predição, campo de arbítrio admissível e arredondamento, esse último limitado a 1% (um por cento), conforme consta no item 6.8.1 da NBR 14653-1:2019 (Avaliação de bens. Parte 1: Procedimentos gerais).

 

 

 

 

Fontes:
CANTEIRO, João Ruy. Construções: seus custos de reprodução na capital de São Paulo de 1939 a 1979; Terrenos: subsídios à técnica de avaliação. 3. ed. São Paulo: Pini, 1980.
DANTAS, Rubens Alves. Engenharia de avaliações: uma introdução à metodologia científica. São Paulo: Pini, 1998.
THOFEHRN, Ragnar. Avaliação de terrenos: por fórmulas matemáticas. São Paulo: Pini, 2008.
HOUAISS, Antônio. Dicionário eletrônico Houaiss da língua portuguesa. Versão 1.0. Editora Objetiva Ltda.: 2001, CD-ROM.