Caso as observações coletadas no mercado imobiliário se refiram a operações feitas a prazo, é necessário transformar converter cada uma das parcelas para o valor presente; a soma de todas as parcelas convertidas para o valor presente representa o valor do terreno para o pagamento à vista ( valor atual ); isso é feito com o auxílio de fórmulas da matemática financeira:
Na fórmula acima i é a taxa real de juros no mercado de capitais; essa taxa inclui a taxa de inflação, como juros compensatórios pelo risco de deterioração do capital, produzida pelo processo inflacionário (MOREIRA, 2001, p. 116).
Considerando que, em 17 de outubro de 2022, a taxa SELIC se encontra em 13,75% e o índice IPCA mais recente referente aos últimos doze meses atingiu 7,17%, então a taxa real de juros é:
Portanto:
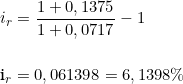
Assim, considerando a taxa real de juros calculada linhas acima, o preço à vista de um terreno vendido por R$100.000,00, com pagamento parcelado em dez prestações fixas anuais, é calculado na tabela abaixo:
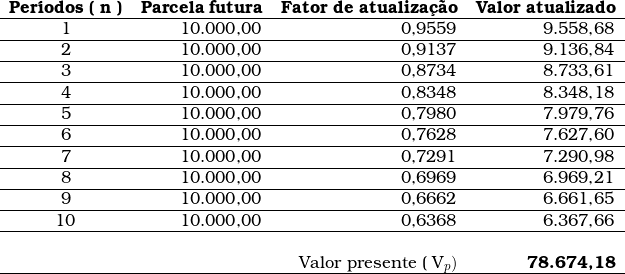
Assim, considerando a taxa real de juros calculada linhas acima, o preço à vista de um terreno vendido por R$100.000,00, com pagamento parcelado em dez prestações fixas anuais, é: R$78.674,18.
Caso as parcelas sejam mensais, então é necessário converter a taxa real de juros anuais para taxa real de juros ao mês; isso é feito com o auxílio da seguinte fórmula:
![[( 1 + i_r )^{\tfrac{1}{12}} ] - 1](https://oficialavaliador.com.br/wp-content/ql-cache/quicklatex.com-394d6700f0b4ec907dd4416c816b0608_l3.png "Rendered by QuickLaTeX.com")
Na exemplo acima, a taxa mensal é:
![[( 1 + 0,061398)^{\tfrac{1}{12}}] - 1 = 0,004978 \quad \therefore \quad 0,4978\%](https://oficialavaliador.com.br/wp-content/ql-cache/quicklatex.com-52b175515b1eb2759c07f96f405fc528_l3.png "Rendered by QuickLaTeX.com")
Se a renda líquida mensal for fixa, então há dois caminhos para se fazerem os cálculos:
a) criar a tabela para a atualização de cada parcela ou
b) calcular o fator de antecipação específico relativo ao número de parcelas futuras que serão antecipadas.
Primeiro modo.
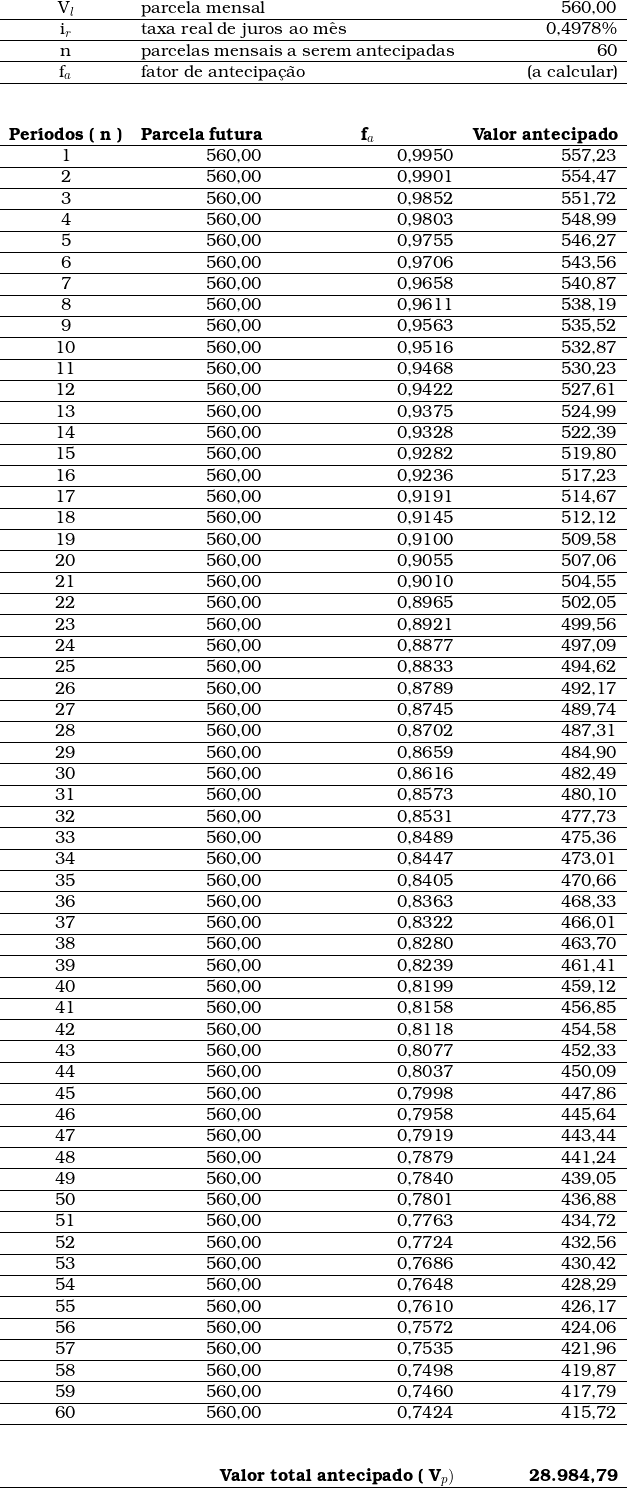
Segundo modo.
Sabendo-se que as parcelas mensais são fixas, então, com o auxílio da fórmula abaixo, temos:
![V_p = V_l ⋅ \Big[ \dfrac{( 1 + i )^n - 1}{i⋅( 1 + i )^n} \Big] \\ \indexspace f_a = \dfrac{( 1 + 0,4978\%)^{60} - 1}{0,4978\%⋅( 1 + 0,4978\%)^{60}} \\ \indexspace \indexspace f_a = \textbf{51,7586}](https://oficialavaliador.com.br/wp-content/ql-cache/quicklatex.com-e06629f35c7b2f60e10a12cc6f32d183_l3.png "Rendered by QuickLaTeX.com")
O exemplo acima encontra-se na planilha desenvolvida, disponível logo abaixo.
Fontes:
KUHNEN, Osmar Leonardo; BAUER, Udibert Reinoldo. 3. ed. Matemática financeira aplicada e análises de investimentos. São Paulo: Atlas, 2001, p. 119.
MOREIRA, Alberto Lélio. Princípios de engenharia e de avaliações. 5. ed. São Paulo: Pini, 2001.
