Quando a homogeneização da amostra é feita por fatores, eles devem ser aplicados na forma de somatório; deve ser registrado que não se faz a homogeneização nem por muiltiplicação de fatores nem por subtração de coeficientes, pois esses dois caminhos distorcem os cálculos. O somatório de fatores será demonstrado abaixo.
Digamos que o elemento que compõe a amostra ( ![]() ) tenha sofrido, em relação ao paradigma (
) tenha sofrido, em relação ao paradigma ( ![]() ), cujo fator é igual 1,00 (um), as seguintes influências:
), cujo fator é igual 1,00 (um), as seguintes influências:
em função da testada, uma valorização de 5% (cinco por cento); desse modo, o respectivo fator é 1,05 (um inteiro e cinco centésimos); e
em função da topografia, uma desvalorização de -10% (dez por cento negativo), desse modo, o respectivo fator é 0,90 (noventa centésimos).
Então sabemos que:
![]()
Prosseguindo:
![]()
Portanto:
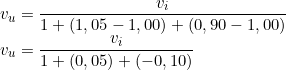
A equação acima demonstra que, na fase de homogeneização, os fatores devem ser aplicados na forma de somatório e de modo invertido (DANTAS, 1998, p. 21).
Conforme THOFEHRN (2008, p. 13), o lote-padrão (paradigma) é o terreno urbano com as seguintes características:
a – formato retangular;
b – frente única em meio de quadra;
c – topografia plana, horizontal e no nível da rua;
d – solo firme e seco;
e – frente (testada) de 10 m e profundidade de 40 m (“fundo-padrão”).
A planilha de homogeneização disponibilizada aplica os fatores na forma de somatório e de modo invertido.
Dinâmica do tratamento de dados por fatores de homogeneização
O conceito de homogeneização está presente no item 3.1.25 da NBR 14653-1:2019, nos seguintes termos:
3.1.25 homogeneização: tratamento dos preços observados, mediante a aplicação de transformações matemáticas que expressem em termos relativos, as diferenças entre os atributos dos dados de mercado e os do bem avaliando
Por sua vez, o conceito de tratamento de dados está presente no item 3.1.44 da mesma norma técnica, nos seguintes termos:
3.1.44 tratamento de dados: aplicação de operações que expressem, em termos relativos, as diferenças de atributos entre os dados de mercado e os do bem avaliando
O primeiro passo no procedimento de homogeneização é identificar quais são os principais atributos que são capazes de explicar a variação de preços dos itens da amostra.
Uma vez identificados, associam-se a esses atributos os fatores relativos a cada item da amostra.
Na hipótese de serem identificados mais de um atributo capaz de explicar a variação de preços; os fatores ( f ) associados a esses atributos deverão ser aplicados na forma de somatório, observando-se a seguinte fórmula:
![]()
ou simplesmente:
![]()
Desse modo:
![]() , o que é equivalente a:
, o que é equivalente a:
![]()
Portanto, a partir do valor unitário observado no mercado, conseguimos estimar o valor unitário do paradigma, o qual servirá como base de cálculo sobre a qual será aplicado o somatório de fatores do bem imóvel avaliando:
![]()
O exemplo abaixo se refere à avaliação de um terreno e, durante a pesquisa feita no mercado, foram identificados seis atributos capazes de explicar a variação de preços. Portanto, foram considerados seis fatores de homogeneização:
f1i = topografia
f2i = consistência do solo
f3i = testada
f4i = profundidade
f5i = forma de pagamento
f6i = frentes múltiplas ou esquina
Onde i representa cada um dos itens da amostra.
Abaixo, demonstra-se o somatório de fatores de cada um dos itens que compõem a amostra.
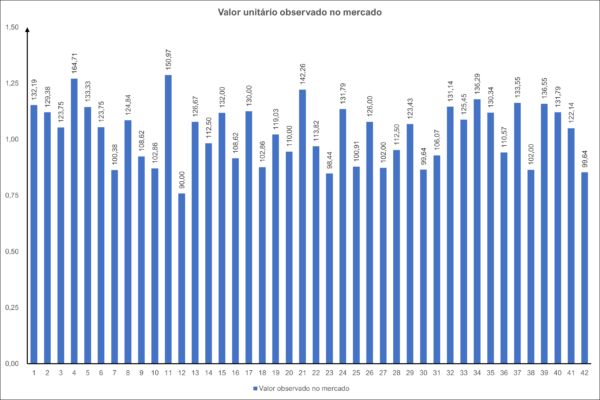
No início dessa análise de dados, temos a seguinte dispersão de dados:
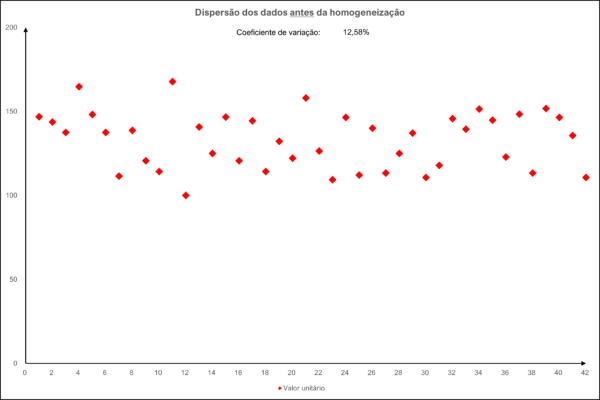
Os fatores utilizados nesta análise serão aqueles associados a cada um desses atributos relevantes já estudados pela doutrina. Os fatores ou foram preestabelecidos em tabelas ou foram calculados por fórmulas amplamente utilizadas na área de avaliação de terrenos.
As planihas para cálculo do somatório de fatores, bem como as tabelas de fatores tabelados, estão disponíveis nesta página.
Uma vez identificados os principais atributos e os fatores a eles associados, estuda-se qual é a situação paradigma. No exemplo utilizado, fixou-se a unidade como sendo o fator de referência. Comparando-se a situação paradigma com o conjunto de dados coletados no mercado, temos o seguinte gráfico.
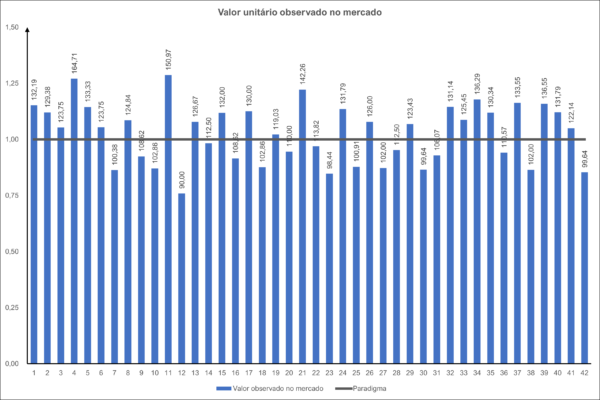
Observe-se que, alguns dados da amostra estão abaixo da referência paradigma enquanto outros dados estão acima da situação paradigma.
Nesse ponto, seguimos a doutrina de Rubens Alves Dantas:
Após a coleta dos elementos que servirão de base para a avaliação, o avaliador geralmente está diante de uma amostra formada por imóveis com características heterogêneas, tornando-se imprescindível a homogeneização dos dados em relação ao bem avaliando, ou a um paradigma adotado, para a utilização adequada do método comparativo. Nesta etapa são retiradas as vantagens ou desvantagens existentes nos dados de referência em relação ao bem avaliando ou a um paradigma adotado. Para isto devem-se utilizar as ferramentas de inferência estatística, através da busca de modelos explicativos do mercado imobiliário.
Quando a homogeneização é feita em relação a um paradigma, o resultado do tratamento estatístico fornece um valor unitário básico. Deve-se observar que, partindo-se do valor unitário básico, para a avaliação do objeto os fatores de homogeneização apresentados devem ser usados de forma invertida. Isto porque, se um TR tem uma vantagem em relação ao paradigma, esta vantagem deve ser retirada na fase de homogeneização; porém, conhecendo-se o valor unitário básico, se um terreno avaliando tem uma vantagem em relação ao paradigma, esta vantagem deve ser dada. É o raciocínio inverso. (DANTAS, 1998, p. 16 e 21).
O ajuste deve ser feito a partir do somatório dos fatores de cada item da amostra à situação paradigma; esse somatório de fatores será aplicado de forma invertida e, portanto, o seu cálculo é feito com base na seguinte fórmula:
![]()
ou de modo simplificado:
![]()
A partir dessa fórmula, identificamos o valor paradigma relativo a cada um dos itens que compõem a amostra e ajustamos os dados observados à situação paradigma; o gráfico seguinte ilustra os resultados das operações matemáticas:
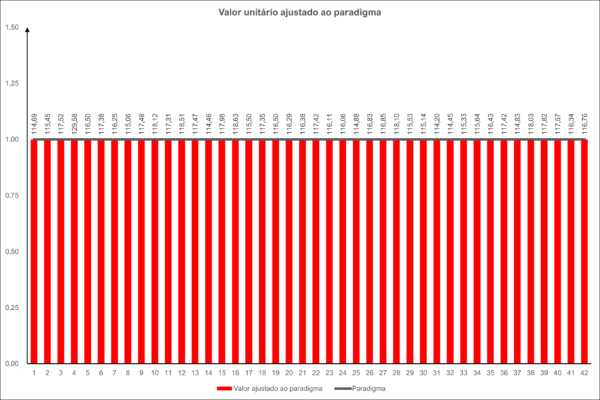
Nesse ponto, os fatores foram ajustados à situação paradigma e os respectivos valores acompanharam esse ajuste; portanto, nessa etapa temos fatores e valores ajustados à situação paradigma.
Esses valores ajustados à situação paradigma servirão como base de cálculo sobre a qual serão aplicados os fatores do bem avaliando, os quais também deverão ser calculados na forma de somatório, porém nesta etapa serão aplicados de forma direta:
![]()
Onde ![]() representa o valor homogeneizado relativo a cada um dos
representa o valor homogeneizado relativo a cada um dos ![]() itens que compõem a amostra.
itens que compõem a amostra.
Assim, chegamos aos resultados seguintes:
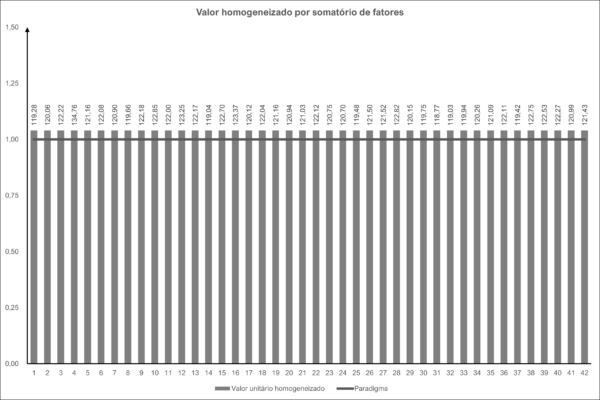
Ao final da fase de homogeneização, temos a seguinte configuração de fatores:
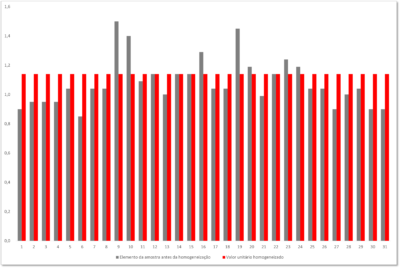
Aqueles elementos cujo somatório de fatores estava abaixo do paradigma, recebeu um acréscimo; por outro lado, aqueles elementos cujo somatório de fatores estava acima do paradigma, sofreu uma redução em seu valor; ao final, todos os elementos ficaram ajustados ao paradigma.
A dispersão dos dados por ser representada pelo gráfico abaixo:

Observe-se que os dados estão menos dispersos e mais próximos da média do conjunto. Isso pode ser comprovado objetivamente a partir da análise do coeficiente de variação ( cv ) que foi reduzido.
No exemplo apresentado acima, o coeficiente de variação foi reduzido de 12,58% para 2,01%, lembrando que:

Esses são os resultados homogeneizados relativos a cada um dos ![]() itens que compõem a amostra, os quais serão posteriormente transferidos para a fase de saneamento da média.
itens que compõem a amostra, os quais serão posteriormente transferidos para a fase de saneamento da média.
Os itens que forem aceitos no saneamento serão, então, levados para o cálculo do intervalo de confiança, grau de precisão e grau de predição.
Embora esses cálculos possam parecer complexos, eles na verdade não o são; as operações matemáticas aplicáveis são básicas; a dificuldade reside simplesmente na quantidade de operações matemáticas exigíveis.
Todavia, esse obstáculo matemático pode ser superado facilmente construindo-se planilhas onde todas as suas células fiquem corretamente vinculadas umas às outras e associadas em fórmulas corretas. Desse modo, os cálculos serão feitos de imediato e os resultados serão transferidos diretamente para a fase de saneamento da média.
Os caminhos para se fazer o saneamento da amostra serão apresentados separadamente; dentre outros, temos:
intervalo de 30% (trinta por cento ) em torno da média
Fontes:
ARLEY, Niels; BUCH, Kai Rander. Introducción a la teoría de la probabilidad y de la estadística. Tradução: Fernando Bombal Gordón. Madrid: Editorial Alhambra S.A., 1968.
CANTEIRO, João Ruy. Construções: seus custos de reprodução na capital de São Paulo de 1939 a 1979; Terrenos: subsídios à técnica de avaliação. 3. ed. São Paulo: Pini, 1980.
DANTAS, Rubens Alves. Engenharia de avaliações: uma introdução à metodologia científica. São Paulo: Pini, 1998.
FIKER, J. Manual de avaliações e perícias em imóveis urbanos. 4. ed. São Paulo: Pini, 2016.
THOFEHRN, Ragnar. Avaliação de terrenos urbanos: por fórmulas matemáticas. São Paulo: Pini, 2008.

