Análise de dados

OBSERVAÇÕES COLETADAS NO MERCADO DO BEM AVALIANDO

Procedimento mais adequado em função da semelhança, ou dessemelhança, entre os comparativos que compõem a amostra.

 

 

\begin{tabular}{p{1cm}p{3cm}p{6cm}p{10cm}} \\ & & \\ \multicolumn{2}{c}{\textbf{Comparativos}} & \textbf{Disponibilidade de dados} & \textbf{Tratamento de dados} \\ & & \\ \hline & & \\ \textbf{1.} & Idênticos & \underline{raro}, porém não impossível & \begin{tabular}{p{10cm}} Procedimento simplificado \\ \textsl{(é necessário certificar)} \end{tabular} & & \\ \hline & & \\ \textbf{2.} & Semelhantes & razoável probabilidade & \begin{tabular}{p{10cm}} {Homogeneização por fatores} \\ Modelo de regressão linear \end{tabular} \\ & & \\ \hline & & \\ \textbf{3.} & Multivariados & alta probabilidade & \begin{tabular}{p{10cm}} Modelo de regressão linear \end{tabular} \\ & & \\ \hline & & & \\ & & & \\ \end{tabular} \\ \\ \begin{tabular}{p{6cm}p{14cm}} \\ \textbf{Tratamento de dados} & \textbf{Etapas mínimas} \\ & \\ {Procedimento simplificado} & \textsl{no mínimo: saneamento da amostra, intervalo de confiança, grau de precisão, grau de predição, campo de arbítrio e arredondamento admissível} \\ & \\ {Homogeneização por fatores} &\textsl{identificação dos fatores, análise objetiva sobre a semelhança, limites de extrapolação, ajuste, homogeneização, saneamento da amostra, intervalo de confiança, grau de precisão, grau de predição, campo de arbítrio e arredondamento} \\ & \\ {Modelo de regressão linear} & \textsl{análise de variância, correlação, erro padrão, limites de extrapolação, análise e eventual exclusão de pontos atípicos, testes estatísticos (heterocedasticidade e correlação serial), análise da normalidade dos resíduos, análise de nível de significância máximo para a rejeição da hipotese nula: dos coeficientes regressores, e do modelo} \\ \end{tabular}

 

 

 

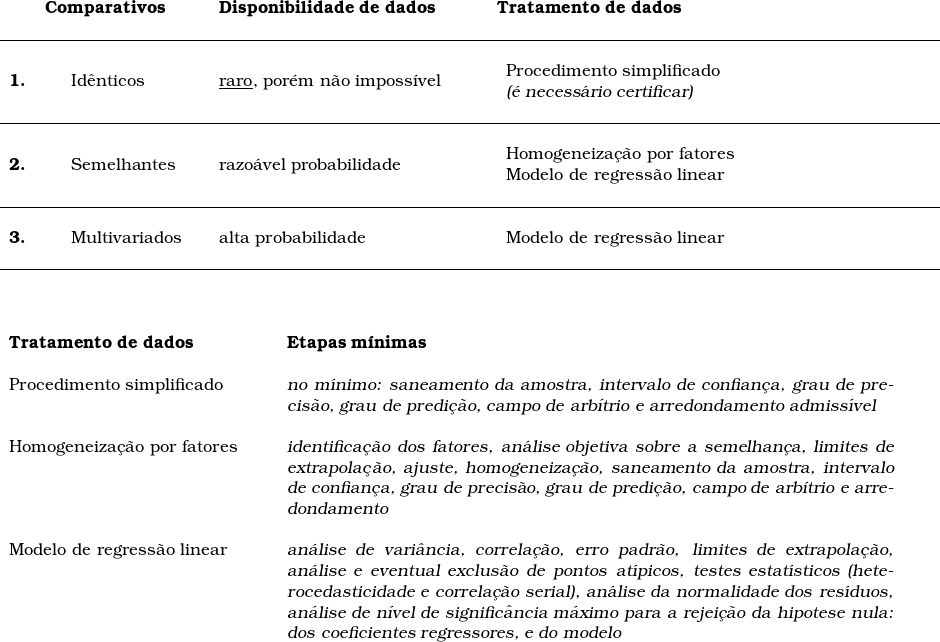
TRATAMENTO DE DADOS POR FATORES DE HOMOGENEIZAÇÃO

 

\begin{tabular}{lrcl} \\ & & & \\ \textbf{Primeira etapa} \\ & & & \\ \textbf{dos elementos → paradigma}: & v_i &=& v_0 \cdot [ 1 + (f_{1} - 1) + (f_{2} - 1) + (f_{3} - 1) + \ldots + (f_{n} - 1)] \\ \\ & v_0 &=& v_i \cdot [ 1 + (f_{1} - 1) + (f_{2} - 1) + (f_{3} - 1) + \ldots + (f_{n} - 1)]^{-1} \\ \\ & v_0 &=& v_i \cdot (\Sigma f_{n} - n + 1)^{-1}\ \textsl{(somatório dos fatores do item da amostra)} \\ & & & \\ & & & \\ & & & \\ \textbf{Segunda etapa} \\ & & & \\ \textbf{do paradigma → bem avaliando}: & v_t &=& v_0 \cdot [ 1 + (f_{1} - 1) + (f_{2} - 1) + (f_{3} - 1) + \ldots + (f_{n} - 1)] \\ \\ & v_t &=& v_0 \cdot (\Sigma f_{n} - n + 1)\ \textsl{(somatório dos fatores do avaliando)} \\ \\ & \\ \\ \multicolumn{1}{r}{Onde}:\ & v_i &=&\ item\ da\ amostra \\ \\ & v_0\ &=&\ valor\ paradigma\ (base\ de\ cálculo\ intermediária) \\ \\ & v_t\ &=&\ bem\ avaliando\ \\ \\ & f\ &=&\ fatores\ de\ homogeneização\ \\ & & & \\ & & & \multicolumn{1}{r}{CANTEIRO (1980, p. 119)} \\ \end{tabular}

 

Uma explicação mais detalhada sobre os passos dessa modalidade de tratamento de dados se encontra nesta página na seção Dinâmica.

 

 

 

TRATAMENTO DE DADOS POR MODELO DE REGRESSÃO LINEAR

Cada item da amostra é interpretado como uma equação em um sistema linear.

 

y_1 = \beta_0 + \beta_1 x_{11} + \beta_2 x_{12} + \beta_3 x_{13}\ldots + \beta_k x_{1k} \\ y_2 = \beta_0 + \beta_1 x_{21} + \beta_2 x_{22} + \beta_3 x_{23}\ldots + \beta_k x_{2k} \\ y_3 = \beta_0 + \beta_1 x_{31} + \beta_2 x_{32} + \beta_3 x_{33}\ldots + \beta_k x_{3k} \\ \vdots y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3}\ldots + \beta_k x_{ik} \\

 

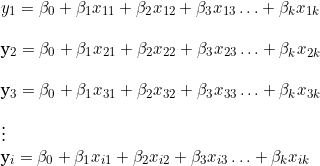
Esse sistema linear será resolvido pelas ferramentas da álgebra matricial, procedimento já apresentado nesta página na seção Álbegra matricial.

Um exemplo dessa solução se encontra nesta página na seção Solução matricial I.

Uma explicação mais detalhada sobre esse procedimento de tratamento de dados está disponível nesta página na seção Regressão linear.