Este é um exemplo de avaliação de bem imóvel, apartamento, em que o tratamento de dados será feito por modelo de regressão linear múltipla.No exemplo, foram coletadas quarenta e oito observações no mercado. Esses dados serão inseridos em um modelo com sete variáveis independentes, também denominadas explanatórias, explicativas; cada uma dessas variávies está relacionada a um atributo específico do imóvel avaliando. O objetivo da análise é medir o impacto que cada um desses atributos exerce sobre a formação do preço do imóvel no mercado, variável dependente.
O tratamento de dados será feito a partir do modelo linear generalizado, qual seja:
![]()
As quarenta e oito observações serão interpretadas como sendo quarenta e oito equações de um sistema linear:
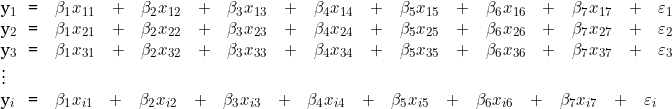
Por inferência estatística, em um modelo de regressão linear múltipla, serão estimados os coeficientes regressores que forneçam a melhor solução possível para o sistema, pelo método dos mínimos quadrados.
O intercepto também será inserido no modelo e, portanto, cada um dos elementos da amostra será assim interpretado:
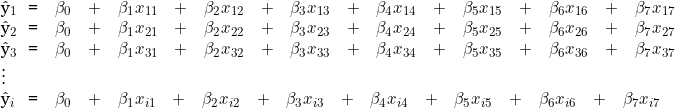
As variáveis inseridas no modelo de análise são:

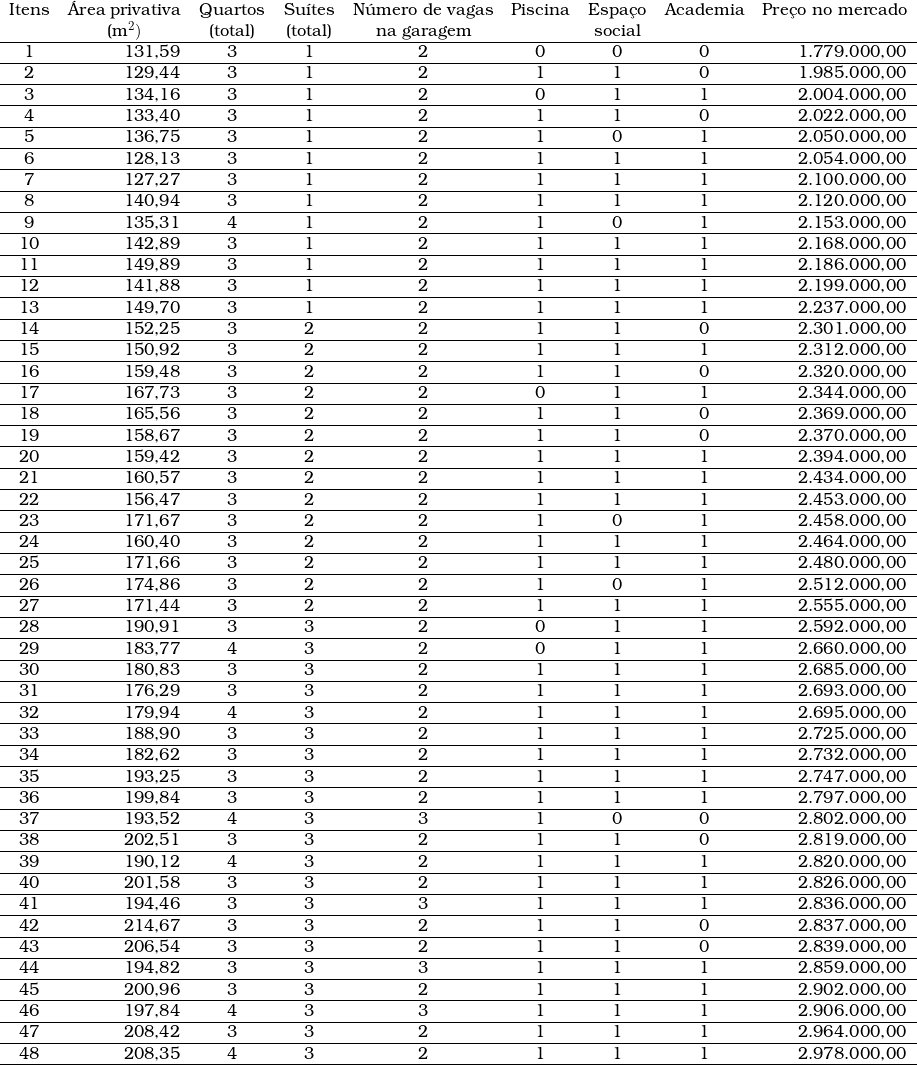
A tabela amostral inicial é a presente:
Fontes:
CHARNET, Reinaldo; FREIRE, Clarice Azevedo de Luna; CHARNET, Eugênia Maria Reginato; BONVINO, Heloísa. Análise de modelos de regressão linear: com aplicações. 2. ed. Campinas,SP: Editora da Unicamp, 2008.
GUJARATI, Damodar. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
______. Econometria: princípios, teoria e aplicações práticas; tradução de Cristina Yamagami; revisão técnica de Salvatore Benito Virgilito. São Paulo: Saraiva Educação, 2019.
NASSER JÚNIOR, Radegaz. Avaliação de bens: princípios básicos e aplicações. 3. ed. São Paulo: Editora Leud, 2019.
OLIVEIRA, Ana Maria de Biazzi Dias; GRANDISKI, Paulo. Métodos científicos e a engenharia de avaliações (com ênfase em inferência estatística). In: Engenharia de avaliações v. 1, 2. ed. São Paulo: Liv. e Ed. Universitária de Direito, 2014.

