NBR 14653-2:2011. Avaliação de bens. Parte 2. Imóveis urbanos. Anexo A (normativo) Procedimentos para a utilização de modelos de regressão linear
A.1 Introdução.
[…]
A.1.2 No modelo linear para representar o mercado, a variável dependente é expressa por uma combinação linear das variáveis independentes, em escala original ou transformadas, e respectivas estimativas dos parâmetros populacionais, acrescida de erro aleatório, oriundo de:
– efeitos de variáveis não detectadas e de variáveis irrelevantes não incluídas no modelo;
– imperfeições acidentais de observação ou de medida;
– variações do comportamento humano, como habilidades diversas de negociação, desejos, necessidades, compulsões, caprichos, ansiedades, diferenças de poder aquisitivo, diferenças culturais, entre outros.
Conceitos
Erro de previsão. Diferença entre os valores reais e os previstos da variável dependente, para cada observação na amostra (ver resíduo) (HAIR JR, 2009, p. 151)
Resíduo ( e ou ε ). Erro na previsão de nossos dados da amostra. Raramente nossas previsões serão perfeitas. Consideramos que o erro aleatório ocorrerá, mas assumimos que esse erro é uma estimativa do verdadeiro erro aleatório na população ( ε ), não apenas o erro na previsão de nossa amostra ( e ). Consideramos que o erro na população que estamos estimando é distribuído com uma média de 0 e uma variância constante (homoscedástica) (Ibidem, p. 153)
O erro 
representa todas aquelas variáveis omitidas no modelo, mas que, coletivamente, afetam 
. Sobre o erro calculado pela regressão, pode-se afirmar:
1. Caráter vago da teoria: a teoria, se é que existe, que explica o comportamento de Y pode ser – e muitas vezes é – incompleta. Poderíamos saber com certeza que a renda semanal de X influencia as despesas de consumo semanais Y, mas podemos desconhecer ou não ter certeza quais são as outras variáveis que afetam Y. Portanto, ui pode ser usado como um substituto para todas as variáveis excluídas ou omitidas do modelo.
2. Falta de dados disponíveis: mesmo sabendo quais são algumas das variáveis excluídas e podendo, portanto, pensar em uma regressão linear múltipla em vez de simples, podemos não contar com informações quantitativas a respeito dessas variáveis. É muito comum, na análise empírica, que os dados que gostaríamos idealmente de incluir não estejam disponíveis. Por exemplo, em princípio, poderíamos incluir a riqueza da família como variável explanatória, além da renda, para explicar as despesas de consumo da família, mas infelizmente essa informação não costuma estar disponível. Portanto, podemos ser obrigados a omitir a variável riqueza de nosso modelo, apesar de sua grande relevância teórica para explicar as despesas de consumo.
3. Variáveis essenciais versus variáveis periféricas: imaginemos que, no nosso exemplo de consumo e renda, além da renda X1, o número de filhos por família X2, o sexo X3, a religião X4, a escolaridade X5 e a localização geográfica X6 também afetem as despesas de consumo. Mas é bem possível que a influência conjunta de todas ou de algumas dessas variáveis seja demasiado pequena e seja, na melhor das hipóteses, não sistematica ou aleatória, de modo que, em termos práticos e tendo em vista os custos, não compense incluí-las explicitamente no modelo. Esperamos que seu efeito combinado possa ser tratado como uma variável aleatória: ui.
4. Caráter intrinsecamente aleatório do comportamento humano: mesmo se conseguirmos incluir todas as variáveis relevantes no modelo, sempre haverá algo de “intrinsecamente” aleatório nos Y individuais que não pode ser explicado por mais que nos esforcemos para isso. Os termos de erro, os u, podem refletir isso bem.
5. Variáveis proxy pouco adequadas: embora o modelo clássico de regressão (que será examinado no Capítulo 3) pressuponha que as variáveis Y e X são medidas com exatidão, na prática os dados podem ser infestados de erros de medição. Considere-se, por exemplo, a conhecida teoria da função de consumo de Milton Friedman. Ele considera o consumo permanente ( Yp ) como uma função de renda permanente ( Xp ). Mas, como os dados relativos a essas variáveis não são diretamente observáveis, na prática, utilizamos variáveis proxy, como consumo corrente (Y ) e renda corrente ( X ), que são observáveis. Como os Y e X observados podem não ser iguais aos Yp e Xp, há um problema de erro de medição. Neste caso, o termo de erro, também pode representar os erros de medição. Como veremos em um capítulo posterior, se existirem tais erros de medição, eles podem ter graves implicações na estimativa dos coeficientes da regressão, os β.
6. Princípio da parcimônia: de acordo com a navalha de Occam, o ideal seria formular o modelo de regressão mais simples possível. Se pudermos explicar parte “substancial” do comportamento de Y com duas ou três variáveis explanatórias e se nossa teoria não for suficientemente forte para sugerir a inclusão de outras variáveis, por que incluir mais variáveis? Melhor deixar que ui represente todas as outras variáveis. Naturalmente, não deveríamos excluir variáveis importantes e relevantes, mas apenas cuidar de formular um modelo regressão simples.
7. Forma funcional equivocada: mesmo se as variáveis explanatorias de um fenômeno forem teoricamente corretas e mesmo se encontrarmos dados para essas variáveis, muitas vezes desconhecemos a forma funcional da relação entre o regressando e os regressores. As despesas de consumo serão uma função (invariável) da renda ou serão uma função não linear (invariável) ? Se for o primeiro caso, Yi – β1 + β2 Xi + ui, será a relação funcional entre Y e X, mas se for o segundo, então Yi = β1 + β2 Xi + β3 X2i + ui, seria a relação cabível. Nos modelos de duas variáveis, a forma funcional da relação pode muitas vezes ser inferida do gráfico de disper~sao. Mas, em um modelo de regressão múltipla, não é fácil determinar a relação funcional adequada, pois não podemos visualizar graficamente diagramas de dispersão com múltiplas dimensões.
Por todas essas razões, o termo erro estocástico ui assume um papel fundamental na analise de regressão, como veremos à medida que formos avançando. (GUJARATI, 2006, p.35-36).
Para o cálculos dos resíduos, podemos considerar as seguintes equações:
Consideremos o seguinte conjunto de dados:
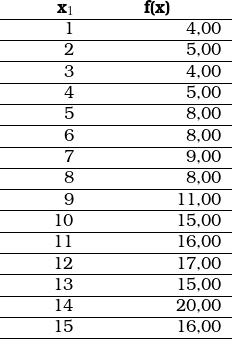
A análise desse conjunto de dados apresentou os seguintes resultados:
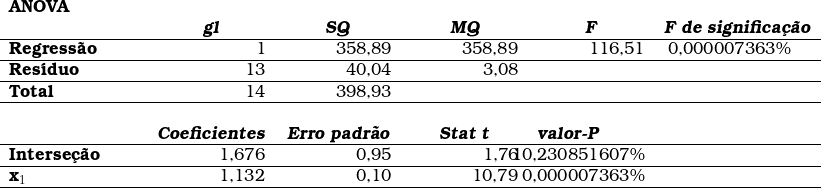
Fazendo os cálculos a partir da equação linear, temos os seguintes valores previstos pela regressão:
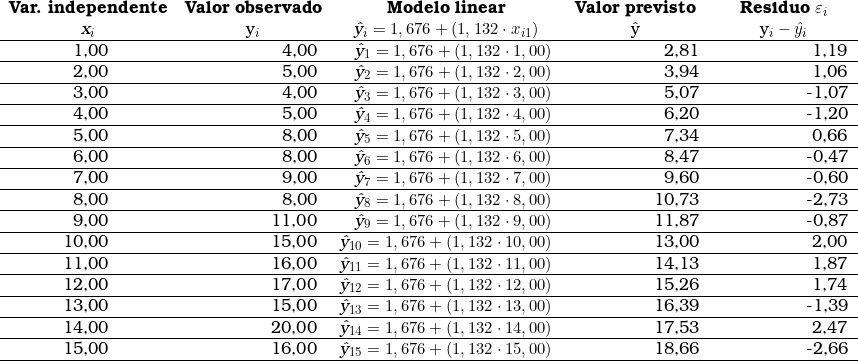
A parcela não explicada pela variável independente corresponde à diferença entre o valor observado e o valor previsto pela regressão. Os valores observados em comparação aos valores previstos pela equação regressão, os quais se encontram perfeitamente alinhados na linha reta, podem ser visualizados no seguinte gráfico:
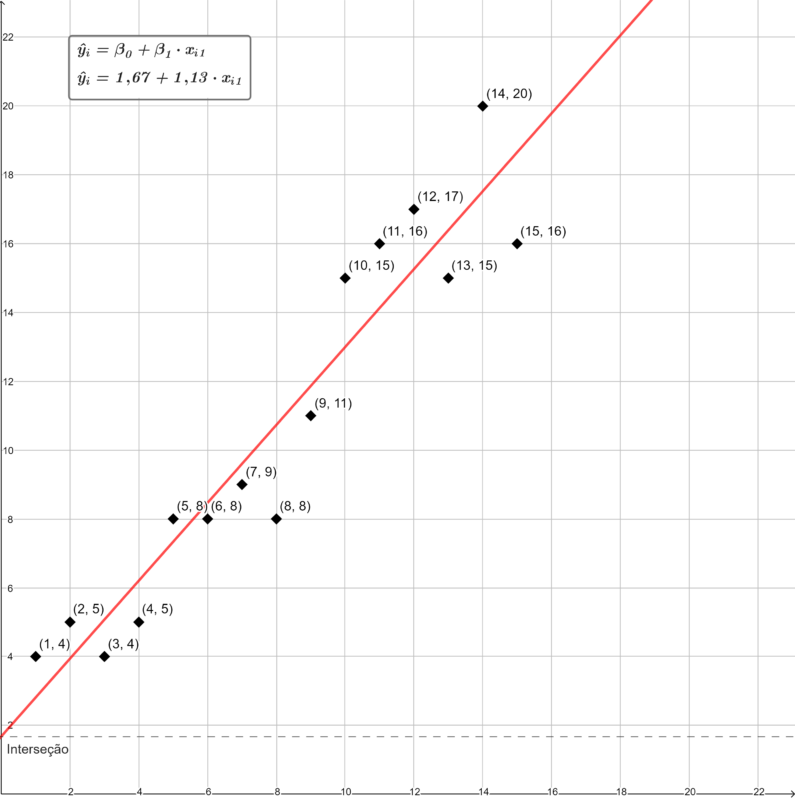
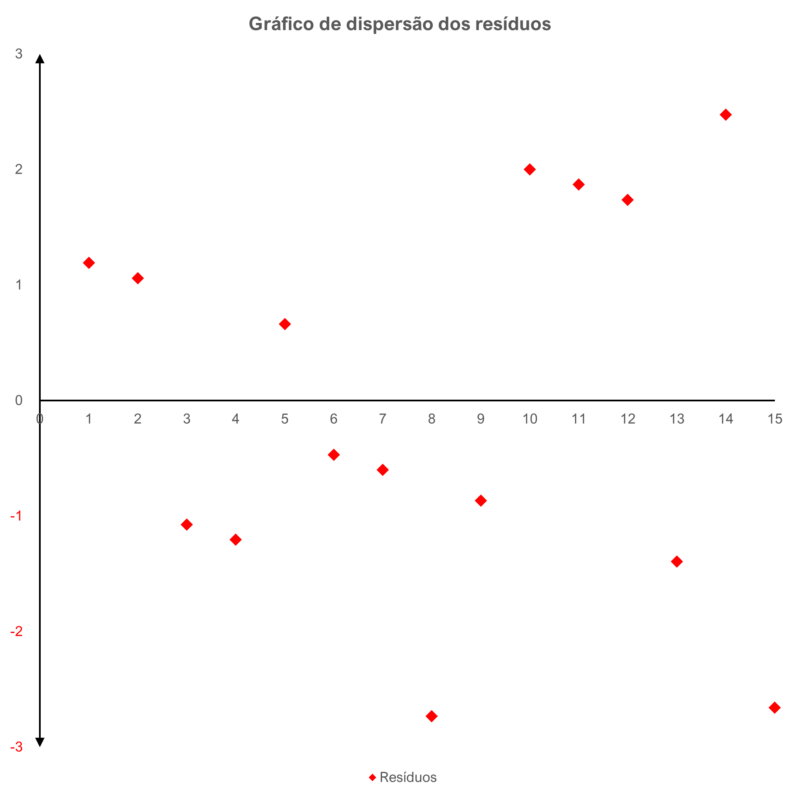
A dispersão dos resíduos em função da variável independente pode ser demonstrada visualmente no gráfico abaixo:
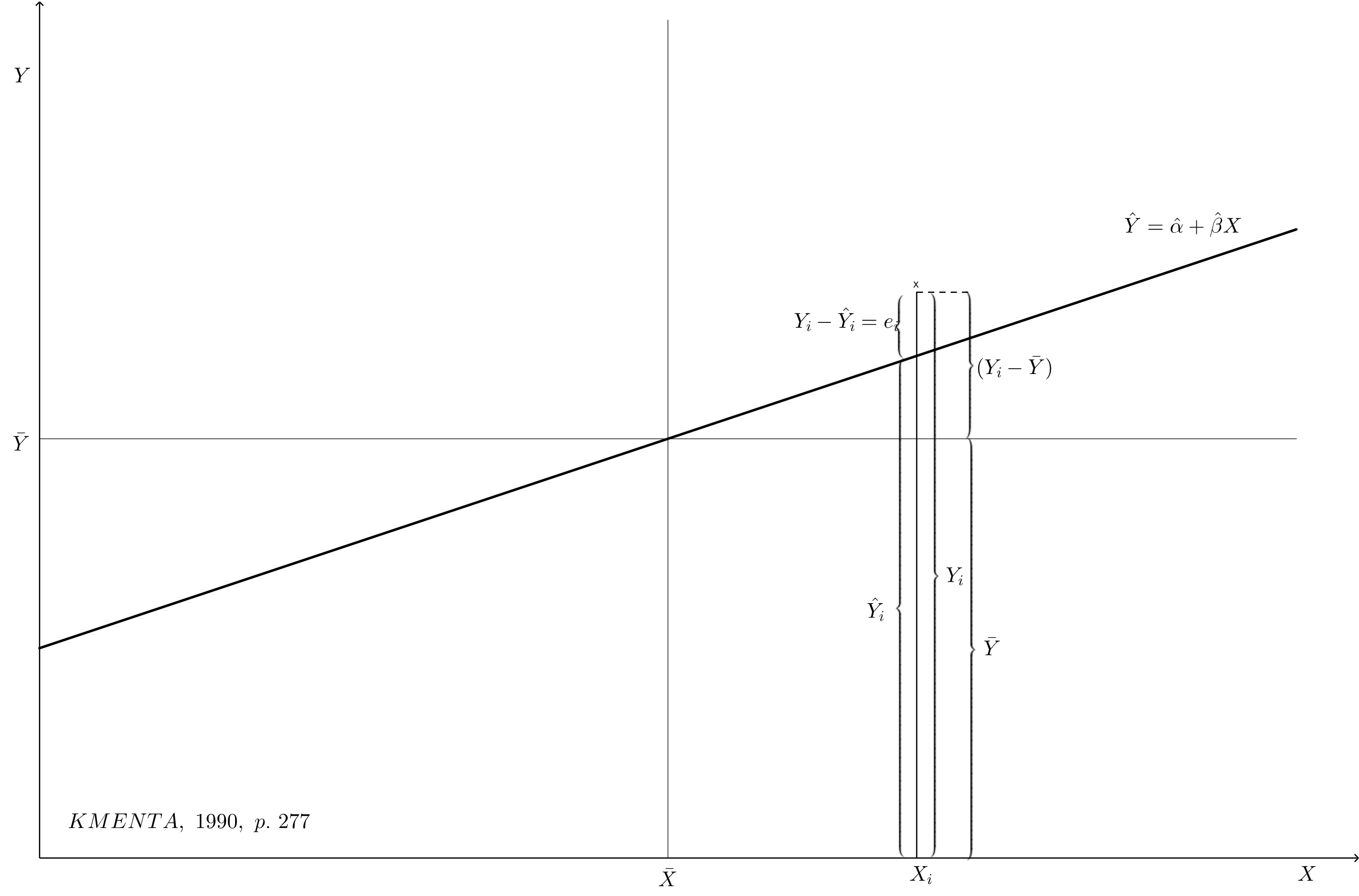
O gráfico de resíduos abaixo (KMENTA, 1990, p. 277) demonstra visualmente o erro aleatório ( e ) e os resíduos da regressão 
.
(1) ![\begin{align*} \sum_i (Y_i - \bar{Y})^2 &= \sum_i [(\hat{Y}_i - \bar{Y}) + e_i]^2 \\ &= \sum_i (\hat{Y}_i - \bar{Y})^2 + \sum_i e_i^2 + 2 \cdot \sum_i (\hat{Y}_i - \bar{Y}) \cdot e_i \end{align*}](https://oficialavaliador.com.br/wp-content/ql-cache/quicklatex.com-229443038892e15d6903c7d119958500_l3.png "Rendered by QuickLaTeX.com")
Consideremos o último termo do segundo membro da equação. Fazendo a substituição de 
, obteremos:
(2) 
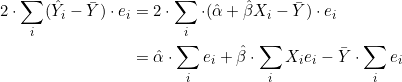
Sendo:
Portanto:
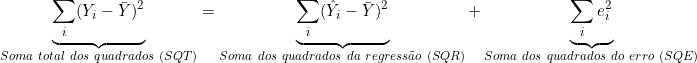
(3) 
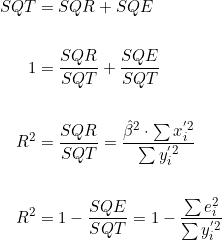
Fontes
ANDERSON, David Ray; SWEENEY, Dennis J.; WILLIAMS, Thomas Arthur. Estatística aplicada à administração e economia. Tradução da 2ª edição norte-americana por Luiz Sérgio de Castro Paiva. São Paulo: Pioneira Thomson Learning, 2003.
ANTON, Howard; RORRES, Chris. Álbegra linear com aplicações [recurso eletrônico]. Porto Alegre: Bookman, 2012.
HAIR JR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.
KMENTA, Jan. Elementos de econometria: teoria econométrica básica. v. 2. São Paulo: Atlas, 1990.
