Correlação não perfeita
No conjunto de dados abaixo, a variável dependente y varia em função da variável independente x; portanto, cada valor das linhas da primeira coluna está correlacionado ao respectivo valor da segunda coluna, porém não de modo exato.
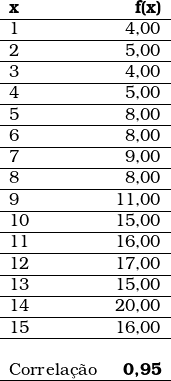
Os coeficientes regressores da equação linear:
são calculados com as seguintes fórmulas:
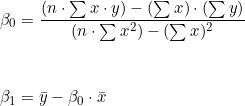
O correlação entre as duas variáveis é positiva, entretanto ela não é perfeita; vale dizer, nem todos os pontos se ajustam perfeitamente à reta da regressão. A dispersão desses dados em relação à reta pode ser visualizada com o auxílio do seguinte gráfico:
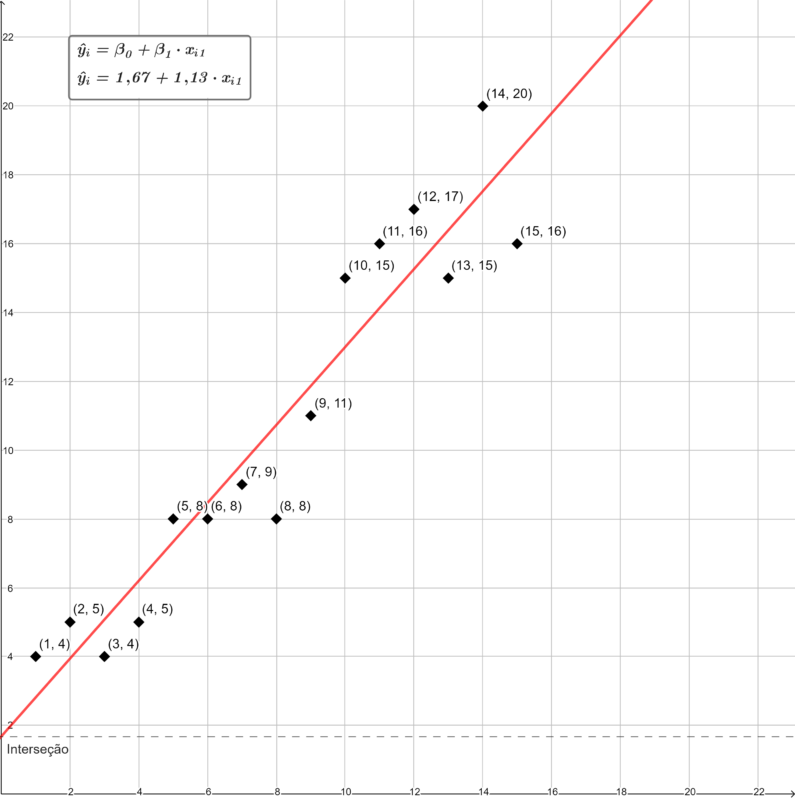
Na análise acima, a equação que melhor se ajusta ao conjunto de dados é:
Aplicando essa equação aos valores da variável independente x1, temos os resultados previstos pela regressão linear. A correlação entre a variável independente e os respectivos valores previstos pela regressão é perfeita.
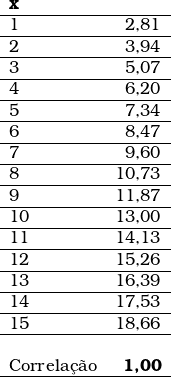
Os resultados previstos ( 
)pela equação de regressão linear não são idênticos aos valores observados ( 
). Essa diferença recebe o nome de resíduos e se refere à parcela não explicada pelas variáveis independentes inseridas no modelo.
Fontes:
CASELLA, George; BERGER, Roger L. Inferência estatística. Tradução de Solange Aparecida Visconte. São Paulo: Cengage Learning, 2018.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
HAIR JUNIOR, Joseph F. et al. Análise multivariada de dados. 6. ed. Tradução de Adonai Schlup Sant’Anna. Porto Alegre: Bookman, 2009.
