Tratamento de dados II | Oficial de Justiça Avaliador

Neste exemplo de avaliação de terreno, os dados foram tratados por fatores de homogeneização.

Foram considerados onze melhoramentos públicos para estudo e homogeneização; o objetivo é estimar o valor do metro quadrado do terreno paradigma a partir dos coeficientes de valorização que foram atribuídos a cada um desses melhoramentos.

$\begin{tabular}{clr} \hline \textbf{Fator} & \multicolumn{1}{c}{\textbf{Atributo}} & \multicolumn{1}{c}{\textbf{Coeficientes}} \\ \hline f_1 & Redes de água potável & 15\% \\ \hline f_2 & Rede de esgoto sanitário & 10\% \\ \hline f_3 & Galerias de águas pluviais & 5\% \\ \hline f_4 & Rede de energia elétrica & 15\% \\ \hline f_5 & Iluminação pública & 5\% \\ \hline f_6 & Guias e sarjetas & 5\% \\ \hline f_7 & Pavimentação & 10\% \\ \hline f_8 & Arborização e jardinagem & 1\% \\ \hline f_9 & Rede telefônica & 5\% \\ \hline f_{10} & Gás de rua & 1\% \\ \hline f_{11} & Transporte coletivo & 10\% \\ \hline \end{tabular}$

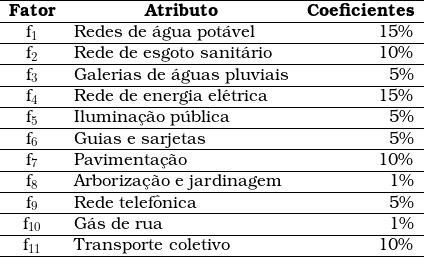
Os fatores serão aplicados na forma de somatório e de modo invertido na etapa de ajuste ao valor paradigma. Nesse ponto, seguimos a doutrina de Dantas (1998, p. 21) segundo o qual:

Quando a homogeneização é feita em relação a um paradigma, o resultado do tratamento estatístico fornece um valor unitário básico. Deve-se observar que, partindo-se do valor unitário básico, para a avaliação do objeto os fatores de homogeneização apresentados devem ser usados de forma invertida. Isto porque, se um TR tem uma vantagem em relação ao paradigma, esta vantagem deve ser retirada na fase de homogeneização; porém, conhecendo-se o valor unitário básico, se um terreno avaliando tem uma vantagem em relação ao paradigma, esta vantagem deve ser dada. É o raciocínio inverso.

Após, na fase final de cálculo da estimativa, os fatores do terreno avaliando serão aplicados na forma de somatório; todo o procedimento observará as seguintes fórmulas:

Relação básica entre coeficientes ( k ) e fatores ( f )

$f = 1 + k$

Somatório de fatores

$\sum f_n = [(f_1 - 1) + (f_2 - 1) + (f_3 - 1) + \ldots + (f_n - 1)] + 1 \\ \indexspace \sum f_n = f_1 + f_2 + f_3 + \ldots + f_n - n + 1$

Ajuste do valor unitário observado ( v_i ) ao valor unitário paradigma ( v_u ), sendo que esse último servirá como base de cálculo para a avaliação

$v_u = \dfrac{v_i}{\sum f_{ni}}$

Aplicação dos fatores próprios do terreno avaliando ( v_t ) sobre a base de cálculo (valor unitário paradigma)

$v_t = v_u \cdot \sum f_{nt}$

A dinâmica do procedimento de homogeneização por fatores está detalhada na página Homogeneização por fatores.

A planilha com esse exemplo de avaliação está disponível logo abaixo:

Tratamento de dados II

Fontes:
CANTEIRO, João Ruy. Construções: seus custos de reprodução na capital de São Paulo de 1939 a 1979; Terrenos: subsídios à técnica de avaliação. 3. ed. São Paulo: Pini, 1980.
DANTAS, Rubens Alves. Engenharia de avaliações: uma introdução à metodologia científica. São Paulo: Pini, 1998.
FIKER, J. Manual de avaliações e perícias em imóveis urbanos. 4. ed. São Paulo: Pini, 2016.
THOFEHRN, Ragnar. Avaliação de terrenos urbanos: por fórmulas matemáticas. São Paulo: Pini, 2008.