Critério baricêntrico

As variáveis independentes que expressam numericamente os atributos de um bem avaliando podem ser capazes de dimensionar o impacto que cada um daqueles atributos exercem sobre a flutuação das respostas que se verificam na variável dependente. Em nosso estudo, a variável de resposta que nos interessa é o valor de mercado do bem avaliando.

Portanto, se os atributos forem relevantes, as variáveis independentes que os expressam não podem ser negligenciadas pelo avaliador e devem ser incluídas no modelo de análise. A ferramenta própria para esse tipo de experimento é a regressão linear múltipla (NBR 14653-2:2011, Anexo A; NBR 14653-3:2019, Anexo A).

Embora sejam analisadas em conjunto, o impacto de cada uma dessas variáveis deve ser quantificado separadamente: em regra, as variáveis não possuem o mesmo nível de significância.

Entretanto, aqueles que aplicam o critério baricêntrico insistem nesse tipo de simplificação por ignorarem os modelos adequados para se analisar a correlação de variáveis de interesse; e esse erro distorce os resultados.

Existem alguns critérios que não são aceitos pela norma brasileira, tais como:
[…]
Critério baricêntrico, onde somamos todos os valores da variável dependente e dividimos pela soma dos valores de cada variável independente. (Nasser  Júnior, 2019, p. 110-112).

 

Prosseguindo, é possível que o mesmo avaliador, usando métodos diferentes, possa encontrar resultados diferentes; é possível também que dois ou mais avaliadores, usando o mesmo método, também encontrem resultados diferentes, pois:

O valor de mercado é um valor bi-lateral por sua natureza, porque implica a existência de um vendedor e de um comprador em um mercado que abrange a grande maioria dos vendedores e compradores de determinadas coisas. As coisas de interesse de limitado número de pessoas ou de grupo de pessoas, não são causa do valor de mercado.
[…]
Dois avaliadores igualmente dotados e idôneos só excepcionalmente encontrarão um mesmo valor único para uma coisa ou imóvel, e isto acontece precisamente por causa dos fatores psicológicos determinantes do valor que são diferentemente apreciados por cada um deles, sem que esses resultados divergentes prejudiquem qualquer das duas avaliações. Cada um dos avaliadores terá os seus justos e fundamentados motivos para chegar à conclusão que externar (Berrini, 1960, p. 29).

 

Porém, causa estranheza o fato de que o mesmo avaliador utilizando o mesmo método encontre resultados diferentes; todavia, é isso o que ocorre quando se aplica o critério baricêntrico.

Caso o tratamento de dados envolva a análise de mais de uma variável independente, o método correto para se fazer o tratamento dos dados é a regressão linear múltipla.

Abaixo, segue um exemplo em que o critério baricêntrico foi aplicado; observe que foram encontrados quatro resultados diferentes.

 

 

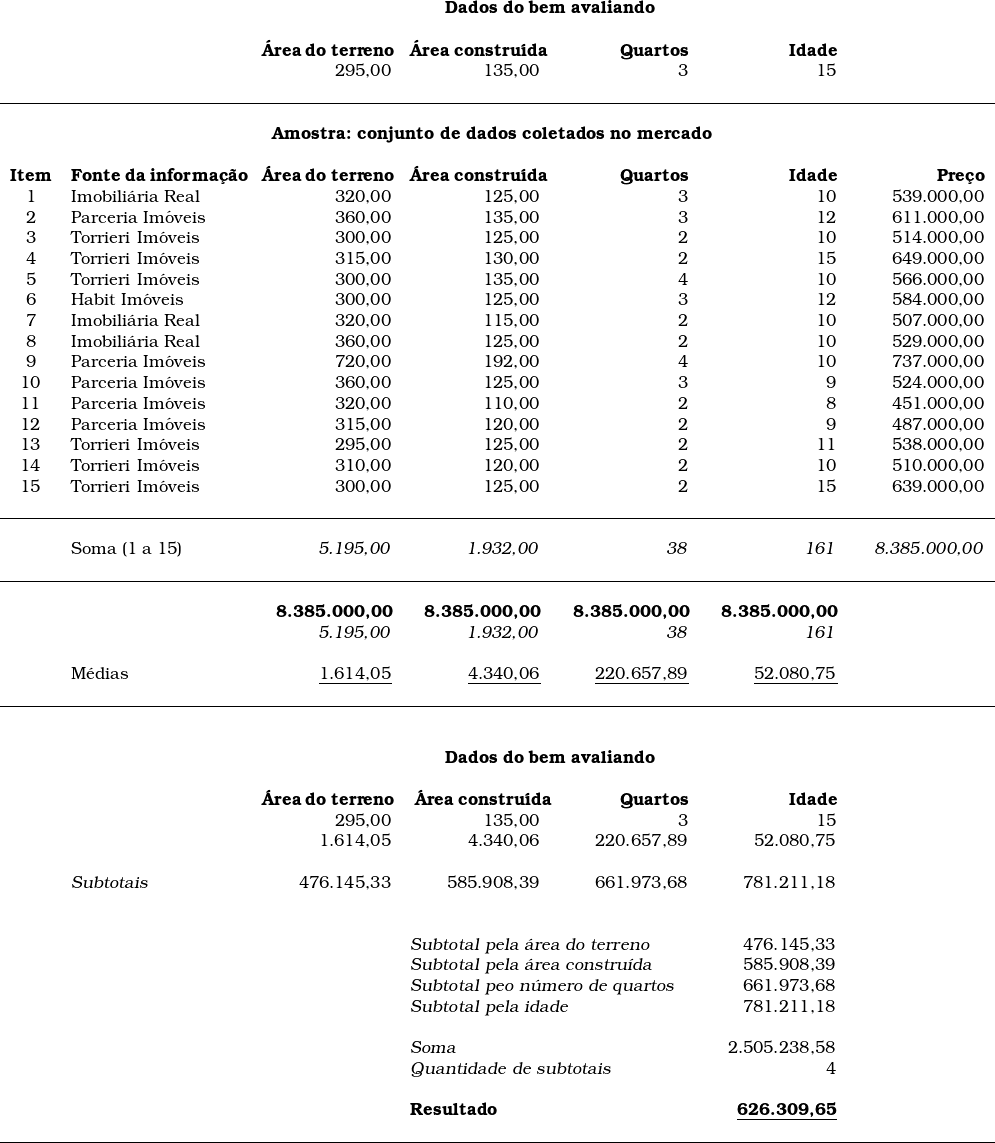
Causa estranheza o fato de que o mesmo avaliador utilizando o mesmo procedimento encontre resultados diferentes; todavia, é isso o que ocorre quando se aplica o critério baricêntrico. No caso de o tratamento de dados envolver a análise de mais de uma variável independente, o método correto para se fazer o tratamento dos dados é a regressão linear múltipla.

A regressão linear é uma ferramenta matemática com a qual se calcula, de modo probabilístico, o impacto que as variáveis independentes, individualmente e em conjunto, causam sobre a variável dependente; em nosso âmbito de atuação, a variável dependente é o valor de mercado do bem.