A NBR 14653-2:2011 apresenta os seguintes conceitos:
3.26 frente de referência: frente da situação paradigma adotada
3.27 frente projetada: projeção da frente real sobre a normal ao menor dos lados ou a corda, no caso de frente em curva
3.28 frente real: comprimento efetivo da linha divisória do imóvel com a via de acesso, em projeção horizontal
[…]
3.67 testada: medida da frente do imóvel
A fórmula básica de Harper-Berrini (Thofern, 2008, p. 53) é:
![]()
![]()
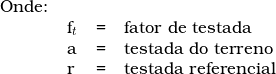
Todavia, o modo de se fazer o cálculo da fator de testada varia conforme três hipóteses, quais sejam:
1ª Hipótese:
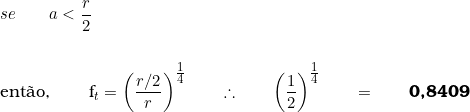
Desse modo, se o menor fator possível é ![]() , então a máxima desvalorização possível, em função do fator de testada, é:
, então a máxima desvalorização possível, em função do fator de testada, é:
![]()
2ª Hipótese:
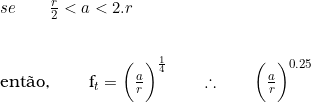
3ª Hipótese:
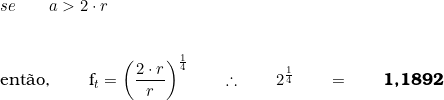
Desse modo, se o maior fator possível é ![]() , então a máxima valorização possível, em função do fator de testada, é:
, então a máxima valorização possível, em função do fator de testada, é:
![]()
A variação do fator de testada pode ser demonstrada visualmente no seguinte gráfico:
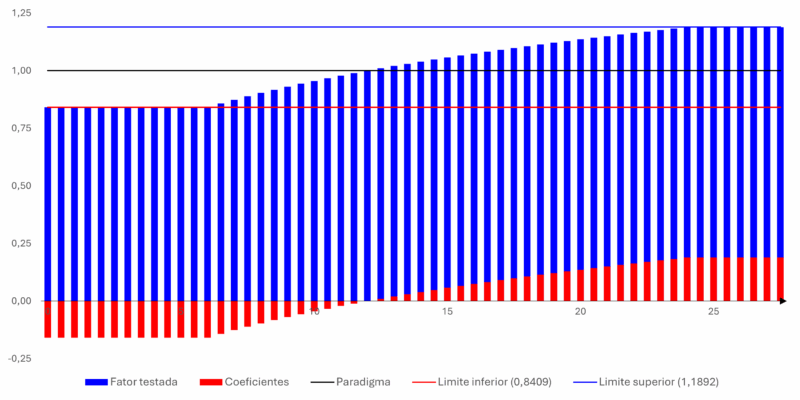
A planilha desenvolvida para o cálculo do fator de testada considera as três hipóteses acima e apresenta resultados para cada uma delas.
Planilha para cálculo do fator de testada
Fontes:
ABUNAHMAN, Sérgio Antônio. Curso básico de engenharia legal e de avaliações. 4. ed. revista e ampliada. São Paulo: Pini, 2008.
FIKER, José. Manual de avaliações e perícias em imóveis urbanos. 4. ed. São Paulo: Pini, 2016.
THOFEHRN, Ragnar. Avaliação de terrenos urbanos: por fórmulas matemáticas. São Paulo: Pini, 2008.
VEGNI-NERI, Guilherme Bomfim. Avaliação de imóveis urbanos e rurais: método prático e moderno. 4. ed. rev., melhorada e atualizada. São Paulo: Ed. Nacional, 1979.

