Esse erro decorre de uma interpretação equivocada, em que se confunde a quantidade de elementos de um conjunto, e a probabilidade de um elemento específico pertencer àquele conjunto, fixados os parâmetros da amostra (média, e desvio-padrão), a um determinado nível de significância.
Para que se demonstre como esse erro interfere nos resultados da avaliação, antes é necessário que consultemos as partes 2 e 3 da norma:
NBR 14653-2:2011 Avaliação de bens. Parte 2: Imóveis urbanos
A.3 Testes de significância
A.3.1 O nível de significância máximo admitido nos demais testes estatísticos (aqueles não citados na Tabela 1) não deve ser superior a 10%.
NBR 14653-3:2019 Avaliação de bens. Parte 3: Imóveis rurais e seus componentes
A.3 Testes de significância
A.3.1 O nível de significância máximo admitido para o teste de hipótese do modelo é de 5% e dos regressores é de 30%. Para os demais testes estatísticos, não pode ser superior a 10%.
O equívoco que se verifica em algumas avaliações decorre de um erro de interpretação, em que se confunde quantidade de dados de um conjunto, e a probabilidade específica de cada um desses dados pertencer a esse conjunto. Aqueles que, equivocadamente, adotam essa prática ordenam os dados em uma sequência crescente; após, excluem os 20% (vinte por cento) primeiros elementos e os 20% (vinte por cento) últimos elementos da amostra.
Por exemplo, em uma amostra com 20 (vinte) elementos, são excluídos os 4 (quatro) primeiros e os 4 (quatro) últimos elementos, ou seja, um total de 8 (oito) de elementos, o que corresponde a 40% (quarenta por cento) da amostra.
Entretanto, observando o nível máximo de significância previsto nos itens A.3.1 da NBR 14653-2:2011 e A.3.1 da NBR 14653-3:2019, em um teste bicaudal, primeiro devem ser calculados os limites de um intervalo de confiança de 90% (noventa por cento); feito isso, seriam excluídos apenas os elementos que ultrapassassem os limites desse intervalo de confiança, ou seja, aqueles valores abaixo do limite inferior, ou aqueles valores acima do limite superior; nesses casos, os elementos estariam posicionados na área de rejeição da hipótese nula. No teste, a hipótese nula corresponde à declaração de que os elementos selecionados pertencem ao conjunto de dados com os parâmetros prefixados.
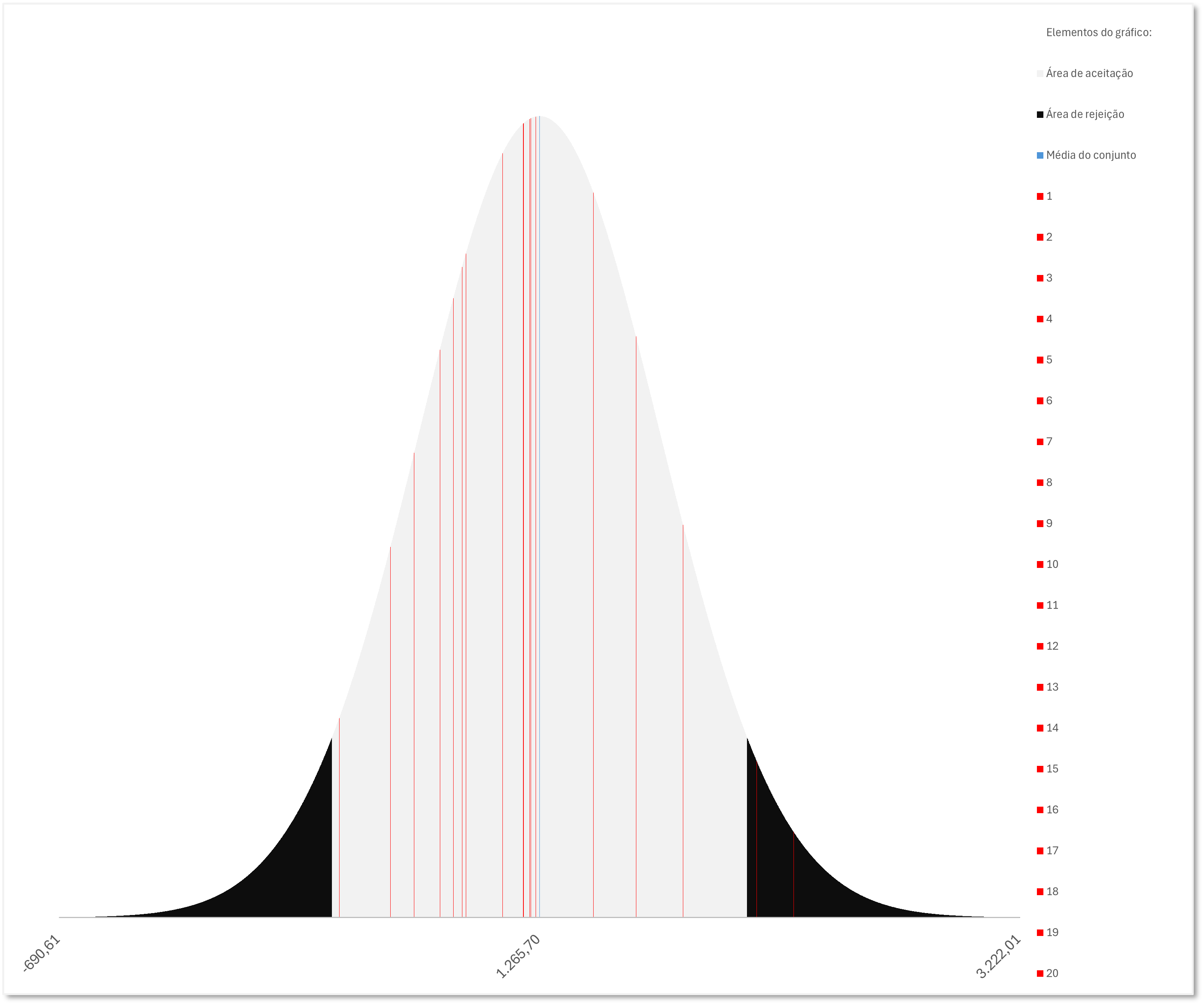
Aceitando-se que os dados seguem a distribuiçõa normal, temos o seguinte gráfico:
No caso acima, apenas os elementos 19 e 20 se posicionaram na área de rejeição da cauda direita, ou seja, eles representam valores maiores que média e superiores ao limite máximo do intervalo de confiança, cuja probabilidade de pertencerem ao conjunto é inferior a 10% (dez por cento) em um teste t bicaudal.
No exemplo acima, somente seriam excluídos esses 2 (dois) últimos elementos, o que corresponde a 10% (dez por cento) do total da amostra
Pelo que se demonstrou acima, não há como afirmar a priori quais elementos deveriam ser excluídos da amostra (conjunto de dados de mercado reunidos para comparação com o imóvel avaliando).
No caso acima, quando se faz o teste de hipótese, é necessário observar que esse teste estatístico específico não consta na Tabela 1 do item 9.2.1 da NBR 14653-2:2011, nem na Tabela 2 do item 9.3.1 da NBR 14653-3:2019. Portanto, nesse caso o nível máximo de significância admitido para a rejeição da hipótese nula é aquele previsto ou no item A.3.1 da NBR 14653-2:2011 (Imóveis urbanos), ou no item A.3.1 da NBR 14653-3:2019 (Imóveis rurais e seus componentes).
No caso do teste acima, a hipótese nula é a própria média amostral, e as possíveis hipóteses alternativas são cada um dos elementos que compõem a amostra; esses elementos devem ser confrontados com a média amostral e testados individualmente. Portanto, o que se busca com esse teste é calcular a probabilidade de que o elemento individualmente considerado pertença, ou não, ao conjunto de dados (amostra).
Estatisticamente, se essa probabilidade ultrapassar o nível de significância ![]() , não se pode rejeitar a hipótese nula (média amostral); desse modo, aceita-se a hipótese nula, afirmando-se que, em um intervalo de confiança de
, não se pode rejeitar a hipótese nula (média amostral); desse modo, aceita-se a hipótese nula, afirmando-se que, em um intervalo de confiança de ![]() , o elemento testado pertence ao conjunto de dados (amostra).
, o elemento testado pertence ao conjunto de dados (amostra).
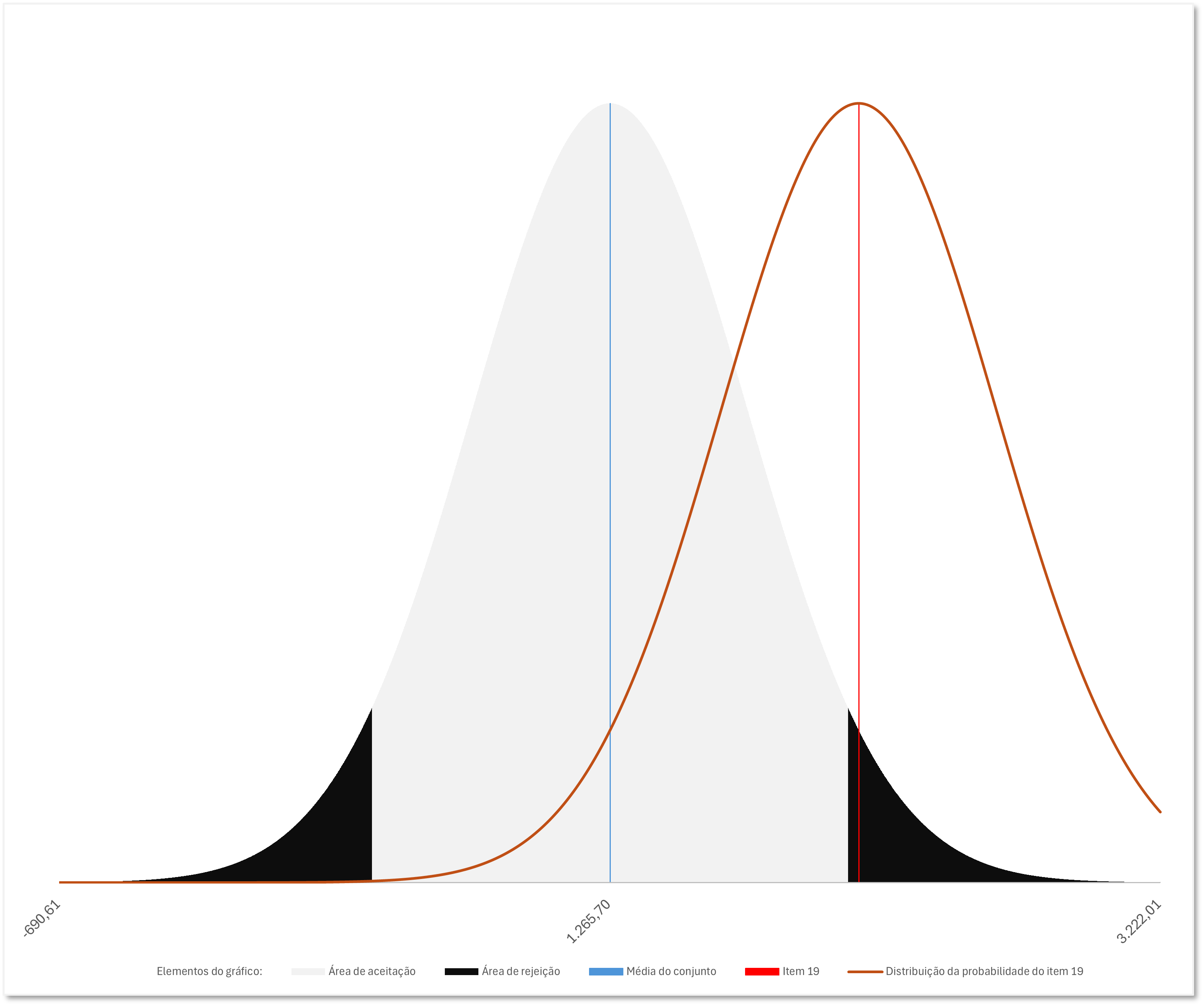
Demonstra-se visualmente o teste relativo ao elemento nº 19 (dezenove) da amostra.
No caso acima, em relação ao elemento nº 19 (dezenove), a sua probabilidade de pertencer ao conjunto de dados foi inferior ao nível de significância ![]() ; portanto, rejeita-se a hipótese nula e afirma-se que, em um intervalo de confiança de
; portanto, rejeita-se a hipótese nula e afirma-se que, em um intervalo de confiança de ![]() , esse elemento não pertence ao conjunto de dados.
, esse elemento não pertence ao conjunto de dados.
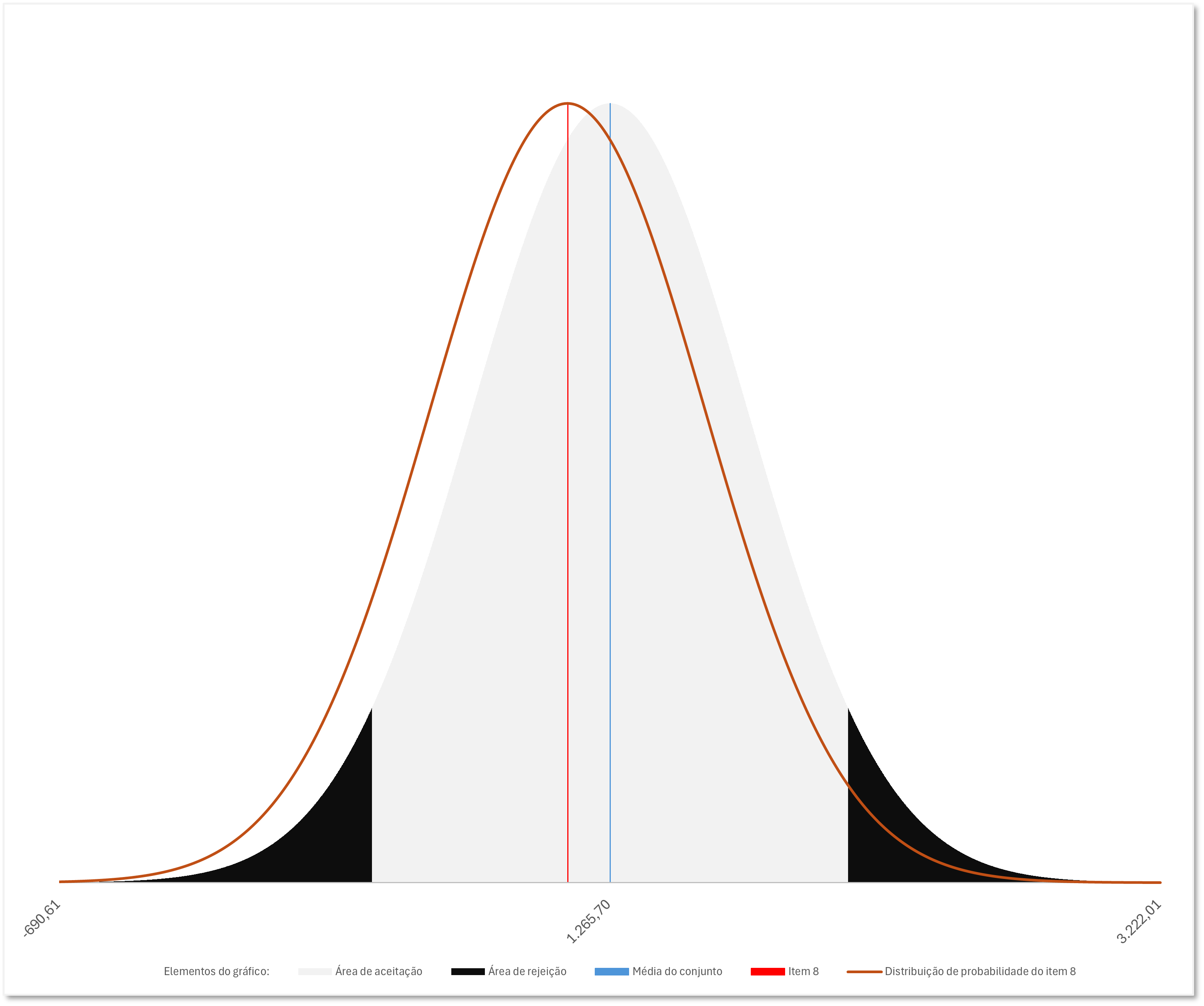
Por sua vez, o teste relativo ao elemento nº 8 (oito) da amostra pode ser demonstrado visualmente no gráfico abaixo.
No caso acima, em relação ao elemento nº 8 (oito), a sua probabilidade de pertencer ao conjunto de dados foi superior ao nível de significância ![]() ; portanto, rejeita-se a hipótese alternativa. Nesse cenário, aceita-se a hipótese alternativa, afirmando-se que, em um intervalo de confiança de
; portanto, rejeita-se a hipótese alternativa. Nesse cenário, aceita-se a hipótese alternativa, afirmando-se que, em um intervalo de confiança de ![]() , esse elemento pertence ao conjunto de dados. Como se vê acima, o elemento nº 8 (oito) se encontra posicionado na área de aceitação do teste.
, esse elemento pertence ao conjunto de dados. Como se vê acima, o elemento nº 8 (oito) se encontra posicionado na área de aceitação do teste.
Fontes:
CASELLA, George; BERGER, Roger L. Inferência estatística. Tradução de Solange Aparecida Visconte. São Paulo: Cengage Learning, 2018.
GUJARATI, Damodar N. Econometria básica. Tradução de Maria José Cyhlar Monteiro. Rio de Janeiro: Elsevier, 2006.
PERES, Fernanda. Estatística aplicada à vida real. Valor de p, nível de significância e testes uni vs. bicaudais. Disponível em: <https://fernandafperes.com.br/blog/valor-de-p-calculo/>. Acesso em: 15 jun. 2024.